Example evaluation of FOCUS Laboratory Data L1 to L3
Johannes Ranke
Last change 18 May 2023 (rebuilt 2023-11-16)
Source:vignettes/FOCUS_L.rmd
FOCUS_L.rmdLaboratory Data L1
The following code defines example dataset L1 from the FOCUS kinetics report, p. 284:
library("mkin", quietly = TRUE)
FOCUS_2006_L1 = data.frame(
t = rep(c(0, 1, 2, 3, 5, 7, 14, 21, 30), each = 2),
parent = c(88.3, 91.4, 85.6, 84.5, 78.9, 77.6,
72.0, 71.9, 50.3, 59.4, 47.0, 45.1,
27.7, 27.3, 10.0, 10.4, 2.9, 4.0))
FOCUS_2006_L1_mkin <- mkin_wide_to_long(FOCUS_2006_L1)Here we use the assumptions of simple first order (SFO), the case of declining rate constant over time (FOMC) and the case of two different phases of the kinetics (DFOP). For a more detailed discussion of the models, please see the FOCUS kinetics report.
Since mkin version 0.9-32 (July 2014), we can use shorthand notation
like "SFO" for parent only degradation models. The
following two lines fit the model and produce the summary report of the
model fit. This covers the numerical analysis given in the FOCUS
report.
## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:13 2023
## Date of summary: Thu Nov 16 04:20:13 2023
##
## Equations:
## d_parent/dt = - k_parent * parent
##
## Model predictions using solution type analytical
##
## Fitted using 133 model solutions performed in 0.011 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 89.85 state
## k_parent 0.10 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 89.850000 -Inf Inf
## log_k_parent -2.302585 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 93.88778 96.5589 -43.94389
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 92.470 1.28200 89.740 95.200
## log_k_parent -2.347 0.03763 -2.428 -2.267
## sigma 2.780 0.46330 1.792 3.767
##
## Parameter correlation:
## parent_0 log_k_parent sigma
## parent_0 1.000e+00 6.186e-01 -1.516e-09
## log_k_parent 6.186e-01 1.000e+00 -3.124e-09
## sigma -1.516e-09 -3.124e-09 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 92.47000 72.13 8.824e-21 89.74000 95.2000
## k_parent 0.09561 26.57 2.487e-14 0.08824 0.1036
## sigma 2.78000 6.00 1.216e-05 1.79200 3.7670
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 3.424 2 7
## parent 3.424 2 7
##
## Estimated disappearance times:
## DT50 DT90
## parent 7.249 24.08
##
## Data:
## time variable observed predicted residual
## 0 parent 88.3 92.471 -4.1710
## 0 parent 91.4 92.471 -1.0710
## 1 parent 85.6 84.039 1.5610
## 1 parent 84.5 84.039 0.4610
## 2 parent 78.9 76.376 2.5241
## 2 parent 77.6 76.376 1.2241
## 3 parent 72.0 69.412 2.5884
## 3 parent 71.9 69.412 2.4884
## 5 parent 50.3 57.330 -7.0301
## 5 parent 59.4 57.330 2.0699
## 7 parent 47.0 47.352 -0.3515
## 7 parent 45.1 47.352 -2.2515
## 14 parent 27.7 24.247 3.4528
## 14 parent 27.3 24.247 3.0528
## 21 parent 10.0 12.416 -2.4163
## 21 parent 10.4 12.416 -2.0163
## 30 parent 2.9 5.251 -2.3513
## 30 parent 4.0 5.251 -1.2513A plot of the fit is obtained with the plot function for mkinfit objects.
plot(m.L1.SFO, show_errmin = TRUE, main = "FOCUS L1 - SFO")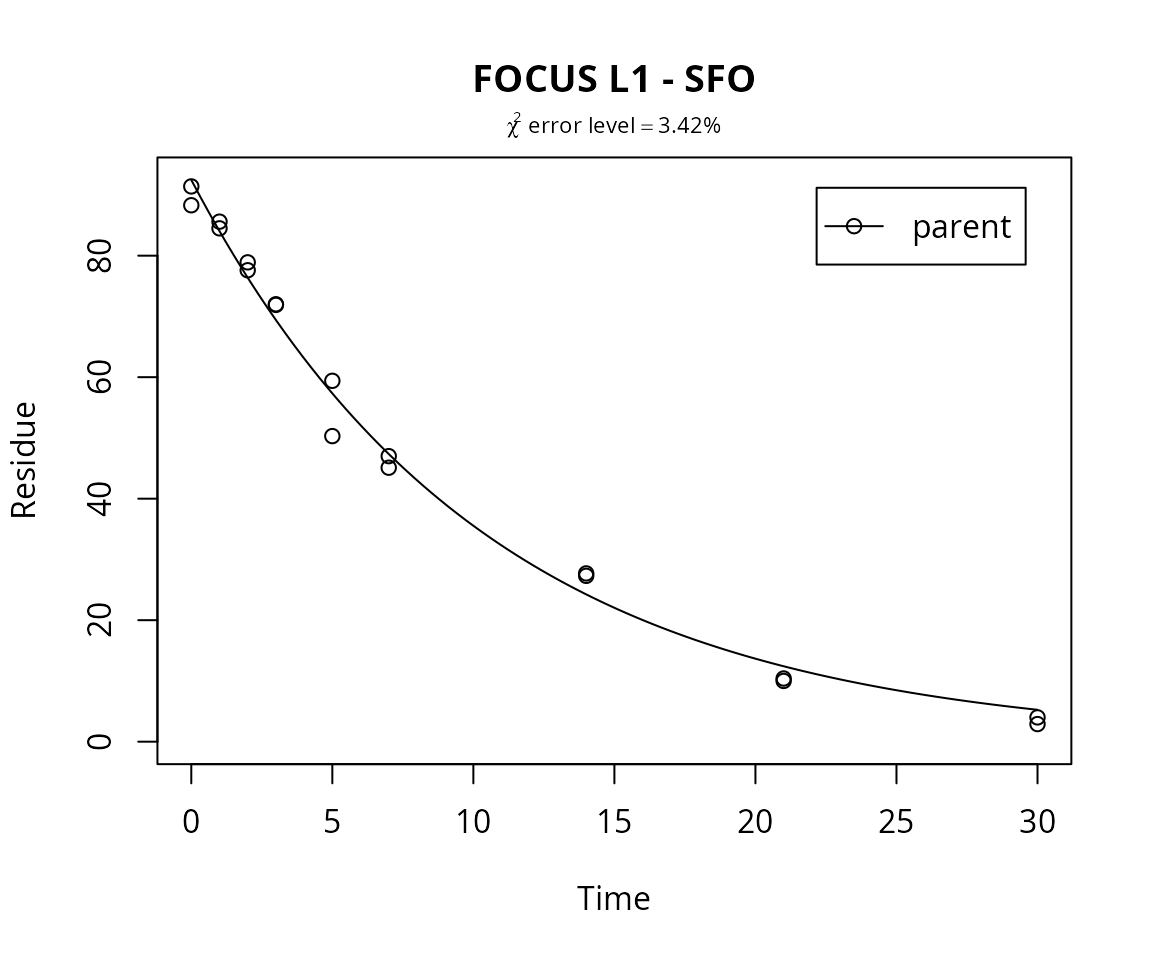
The residual plot can be easily obtained by
mkinresplot(m.L1.SFO, ylab = "Observed", xlab = "Time")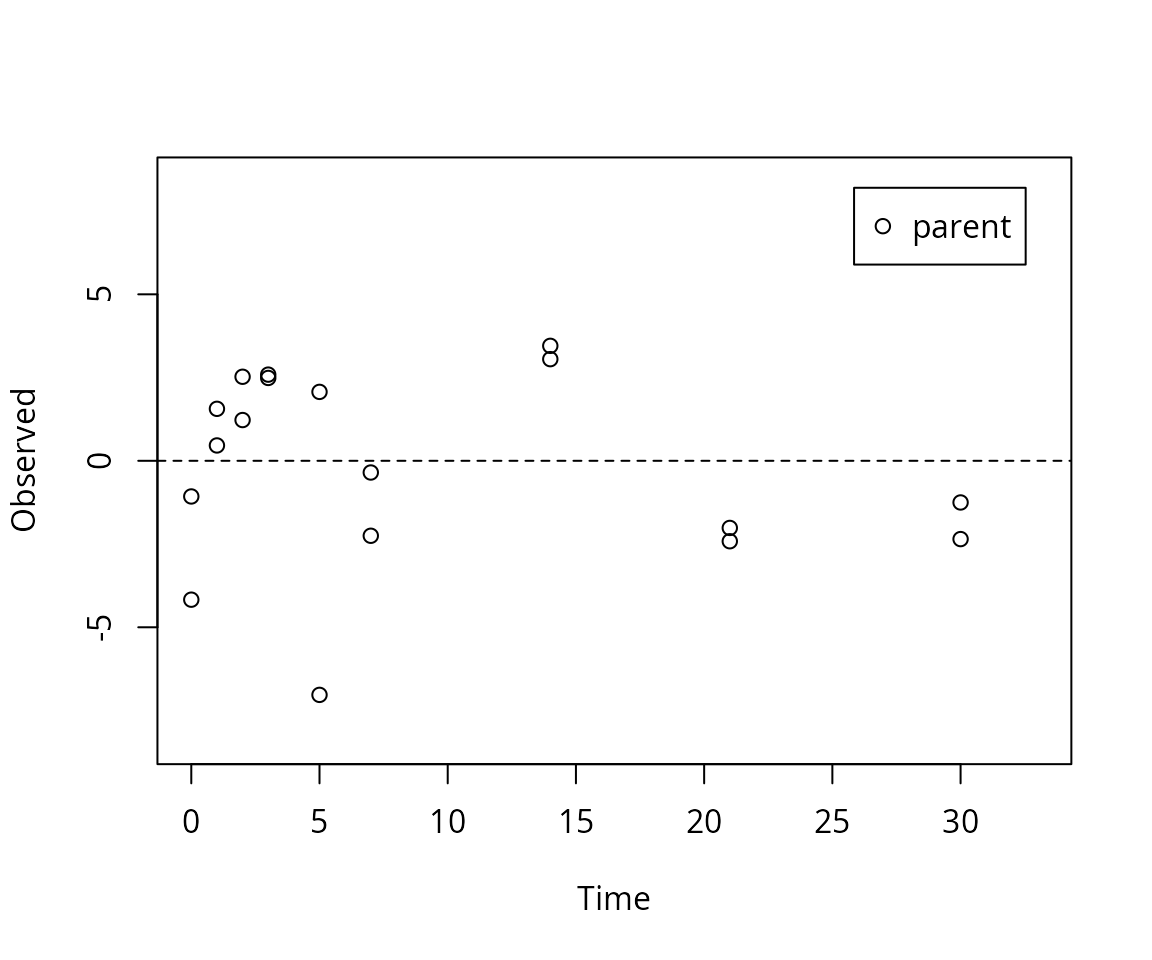
For comparison, the FOMC model is fitted as well, and the \(\chi^2\) error level is checked.
m.L1.FOMC <- mkinfit("FOMC", FOCUS_2006_L1_mkin, quiet=TRUE)## Warning in mkinfit("FOMC", FOCUS_2006_L1_mkin, quiet = TRUE): Optimisation did not converge:
## false convergence (8)
plot(m.L1.FOMC, show_errmin = TRUE, main = "FOCUS L1 - FOMC")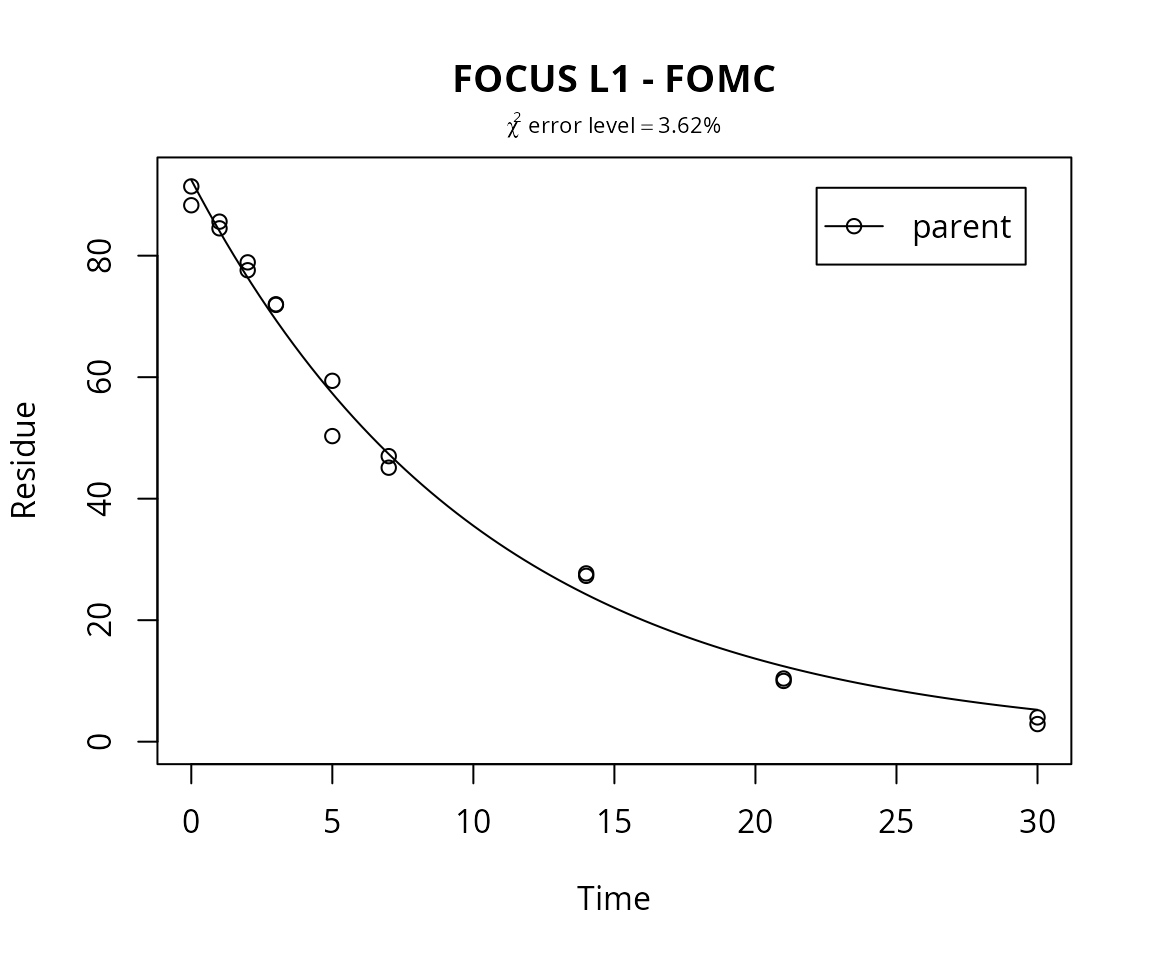
summary(m.L1.FOMC, data = FALSE)## Warning in sqrt(diag(covar)): NaNs produced## Warning in sqrt(1/diag(V)): NaNs produced## Warning in cov2cor(ans$covar): diag(.) had 0 or NA entries; non-finite result
## is doubtful## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:13 2023
## Date of summary: Thu Nov 16 04:20:13 2023
##
## Equations:
## d_parent/dt = - (alpha/beta) * 1/((time/beta) + 1) * parent
##
## Model predictions using solution type analytical
##
## Fitted using 342 model solutions performed in 0.023 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 89.85 state
## alpha 1.00 deparm
## beta 10.00 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 89.850000 -Inf Inf
## log_alpha 0.000000 -Inf Inf
## log_beta 2.302585 -Inf Inf
##
## Fixed parameter values:
## None
##
##
## Warning(s):
## Optimisation did not converge:
## false convergence (8)
##
## Results:
##
## AIC BIC logLik
## 95.88782 99.44931 -43.94391
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 92.47 1.2820 89.720 95.220
## log_alpha 13.20 NaN NaN NaN
## log_beta 15.54 NaN NaN NaN
## sigma 2.78 0.4607 1.792 3.768
##
## Parameter correlation:
## parent_0 log_alpha log_beta sigma
## parent_0 1.000000 NaN NaN 0.000603
## log_alpha NaN 1 NaN NaN
## log_beta NaN NaN 1 NaN
## sigma 0.000603 NaN NaN 1.000000
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 9.247e+01 NA NA 89.720 95.220
## alpha 5.386e+05 NA NA NA NA
## beta 5.633e+06 NA NA NA NA
## sigma 2.780e+00 NA NA 1.792 3.768
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 3.619 3 6
## parent 3.619 3 6
##
## Estimated disappearance times:
## DT50 DT90 DT50back
## parent 7.249 24.08 7.249We get a warning that the default optimisation algorithm
Port did not converge, which is an indication that the
model is overparameterised, i.e. contains too many parameters
that are ill-defined as a consequence.
And in fact, due to the higher number of parameters, and the lower
number of degrees of freedom of the fit, the \(\chi^2\) error level is actually higher for
the FOMC model (3.6%) than for the SFO model (3.4%). Additionally, the
parameters log_alpha and log_beta internally
fitted in the model have excessive confidence intervals, that span more
than 25 orders of magnitude (!) when backtransformed to the scale of
alpha and beta. Also, the t-test for
significant difference from zero does not indicate such a significant
difference, with p-values greater than 0.1, and finally, the parameter
correlation of log_alpha and log_beta is
1.000, clearly indicating that the model is overparameterised.
The \(\chi^2\) error levels reported in Appendix 3 and Appendix 7 to the FOCUS kinetics report are rounded to integer percentages and partly deviate by one percentage point from the results calculated by mkin. The reason for this is not known. However, mkin gives the same \(\chi^2\) error levels as the kinfit package and the calculation routines of the kinfit package have been extensively compared to the results obtained by the KinGUI software, as documented in the kinfit package vignette. KinGUI was the first widely used standard package in this field. Also, the calculation of \(\chi^2\) error levels was compared with KinGUII, CAKE and DegKin manager in a project sponsored by the German Umweltbundesamt (Ranke 2014).
Laboratory Data L2
The following code defines example dataset L2 from the FOCUS kinetics report, p. 287:
FOCUS_2006_L2 = data.frame(
t = rep(c(0, 1, 3, 7, 14, 28), each = 2),
parent = c(96.1, 91.8, 41.4, 38.7,
19.3, 22.3, 4.6, 4.6,
2.6, 1.2, 0.3, 0.6))
FOCUS_2006_L2_mkin <- mkin_wide_to_long(FOCUS_2006_L2)SFO fit for L2
Again, the SFO model is fitted and the result is plotted. The
residual plot can be obtained simply by adding the argument
show_residuals to the plot command.
m.L2.SFO <- mkinfit("SFO", FOCUS_2006_L2_mkin, quiet=TRUE)
plot(m.L2.SFO, show_residuals = TRUE, show_errmin = TRUE,
main = "FOCUS L2 - SFO")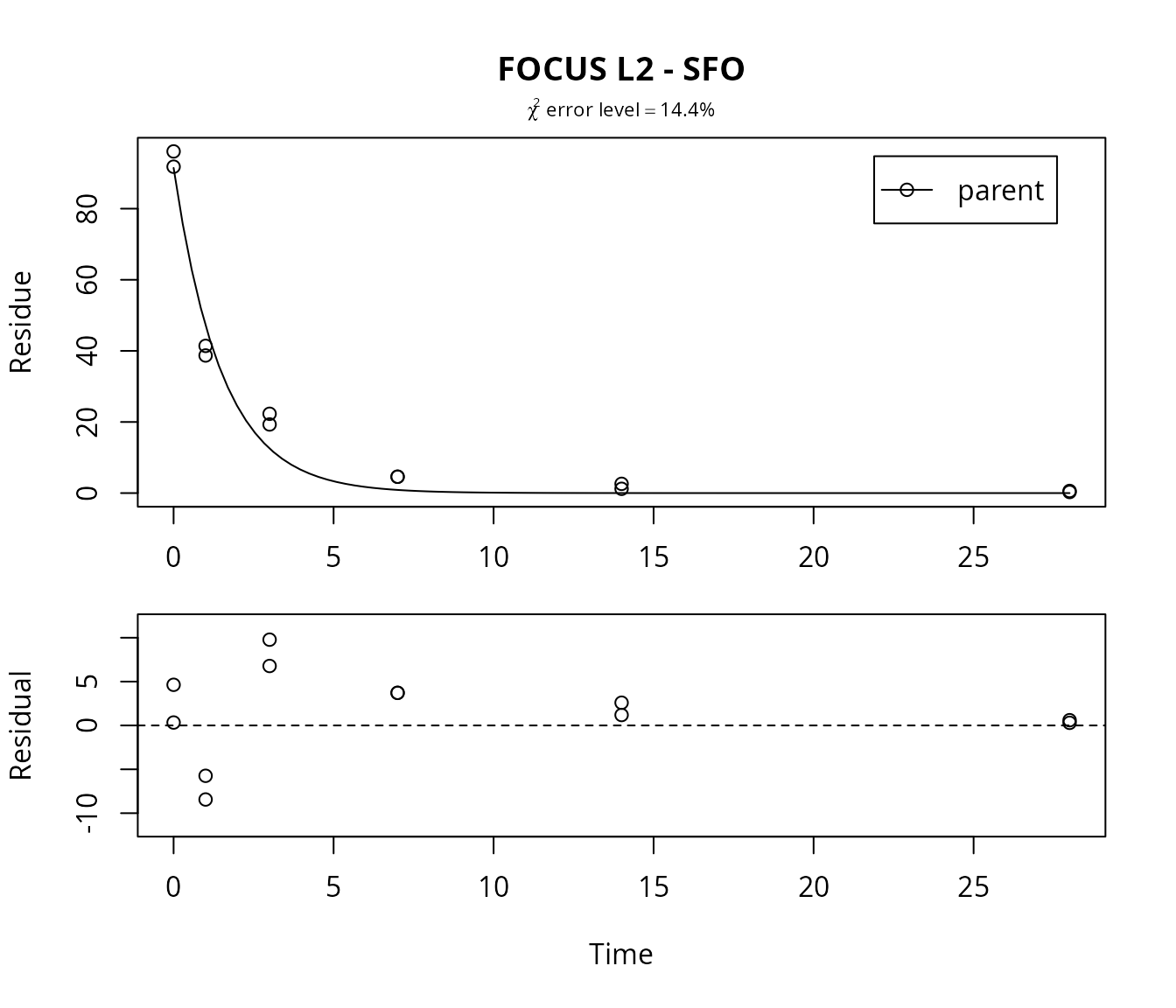
The \(\chi^2\) error level of 14% suggests that the model does not fit very well. This is also obvious from the plots of the fit, in which we have included the residual plot.
In the FOCUS kinetics report, it is stated that there is no apparent systematic error observed from the residual plot up to the measured DT90 (approximately at day 5), and there is an underestimation beyond that point.
We may add that it is difficult to judge the random nature of the residuals just from the three samplings at days 0, 1 and 3. Also, it is not clear a priori why a consistent underestimation after the approximate DT90 should be irrelevant. However, this can be rationalised by the fact that the FOCUS fate models generally only implement SFO kinetics.
FOMC fit for L2
For comparison, the FOMC model is fitted as well, and the \(\chi^2\) error level is checked.
m.L2.FOMC <- mkinfit("FOMC", FOCUS_2006_L2_mkin, quiet = TRUE)
plot(m.L2.FOMC, show_residuals = TRUE,
main = "FOCUS L2 - FOMC")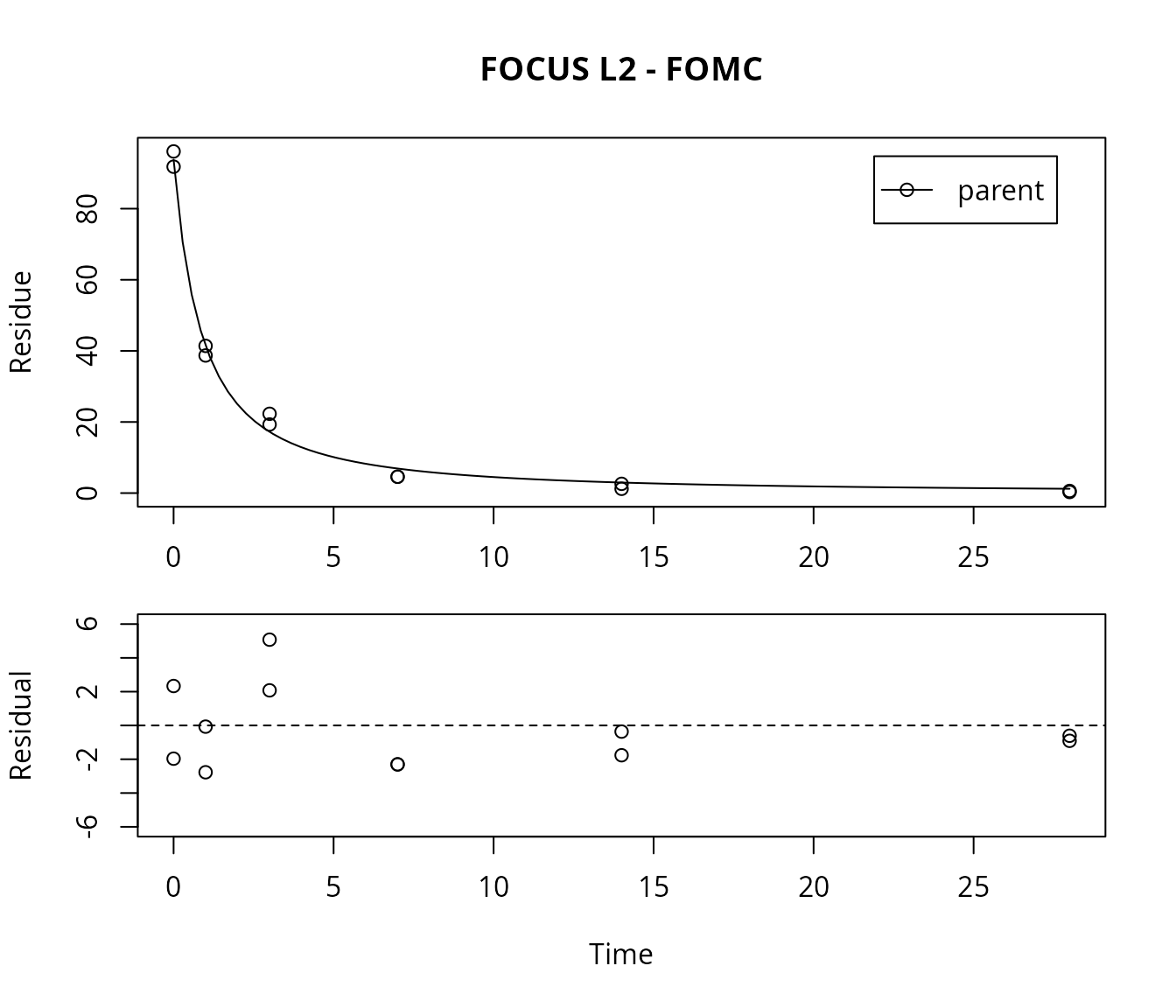
summary(m.L2.FOMC, data = FALSE)## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:13 2023
## Date of summary: Thu Nov 16 04:20:14 2023
##
## Equations:
## d_parent/dt = - (alpha/beta) * 1/((time/beta) + 1) * parent
##
## Model predictions using solution type analytical
##
## Fitted using 239 model solutions performed in 0.014 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 93.95 state
## alpha 1.00 deparm
## beta 10.00 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 93.950000 -Inf Inf
## log_alpha 0.000000 -Inf Inf
## log_beta 2.302585 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 61.78966 63.72928 -26.89483
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 93.7700 1.6130 90.05000 97.4900
## log_alpha 0.3180 0.1559 -0.04149 0.6776
## log_beta 0.2102 0.2493 -0.36460 0.7850
## sigma 2.2760 0.4645 1.20500 3.3470
##
## Parameter correlation:
## parent_0 log_alpha log_beta sigma
## parent_0 1.000e+00 -1.151e-01 -2.085e-01 -7.436e-09
## log_alpha -1.151e-01 1.000e+00 9.741e-01 -1.617e-07
## log_beta -2.085e-01 9.741e-01 1.000e+00 -1.386e-07
## sigma -7.436e-09 -1.617e-07 -1.386e-07 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 93.770 58.120 4.267e-12 90.0500 97.490
## alpha 1.374 6.414 1.030e-04 0.9594 1.969
## beta 1.234 4.012 1.942e-03 0.6945 2.192
## sigma 2.276 4.899 5.977e-04 1.2050 3.347
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 6.205 3 3
## parent 6.205 3 3
##
## Estimated disappearance times:
## DT50 DT90 DT50back
## parent 0.8092 5.356 1.612The error level at which the \(\chi^2\) test passes is much lower in this case. Therefore, the FOMC model provides a better description of the data, as less experimental error has to be assumed in order to explain the data.
DFOP fit for L2
Fitting the four parameter DFOP model further reduces the \(\chi^2\) error level.
m.L2.DFOP <- mkinfit("DFOP", FOCUS_2006_L2_mkin, quiet = TRUE)
plot(m.L2.DFOP, show_residuals = TRUE, show_errmin = TRUE,
main = "FOCUS L2 - DFOP")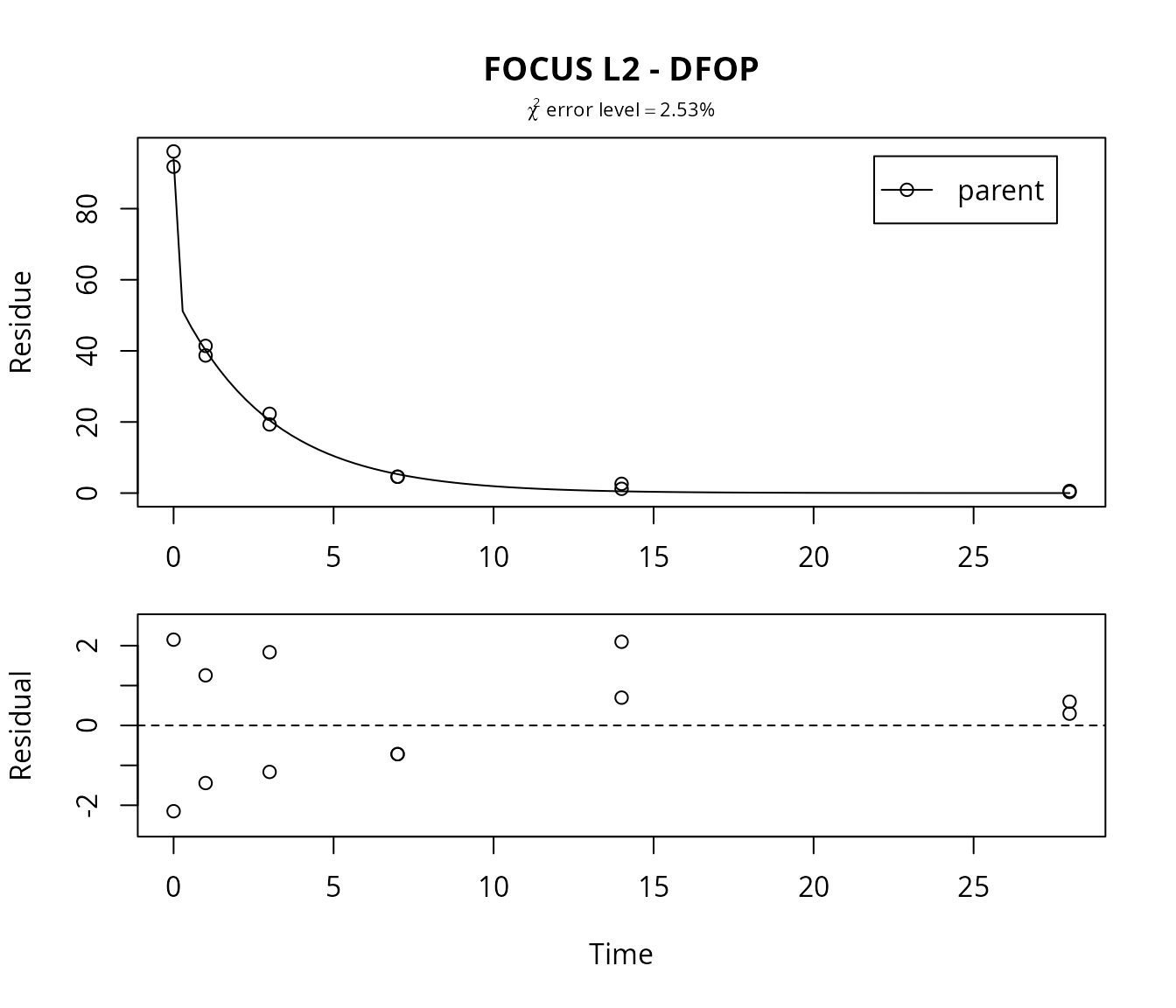
summary(m.L2.DFOP, data = FALSE)## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:14 2023
## Date of summary: Thu Nov 16 04:20:14 2023
##
## Equations:
## d_parent/dt = - ((k1 * g * exp(-k1 * time) + k2 * (1 - g) * exp(-k2 *
## time)) / (g * exp(-k1 * time) + (1 - g) * exp(-k2 * time)))
## * parent
##
## Model predictions using solution type analytical
##
## Fitted using 581 model solutions performed in 0.041 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 93.95 state
## k1 0.10 deparm
## k2 0.01 deparm
## g 0.50 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 93.950000 -Inf Inf
## log_k1 -2.302585 -Inf Inf
## log_k2 -4.605170 -Inf Inf
## g_qlogis 0.000000 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 52.36695 54.79148 -21.18347
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 93.950 9.998e-01 91.5900 96.3100
## log_k1 3.113 1.849e+03 -4369.0000 4375.0000
## log_k2 -1.088 6.285e-02 -1.2370 -0.9394
## g_qlogis -0.399 9.946e-02 -0.6342 -0.1638
## sigma 1.414 2.886e-01 0.7314 2.0960
##
## Parameter correlation:
## parent_0 log_k1 log_k2 g_qlogis sigma
## parent_0 1.000e+00 6.763e-07 -8.944e-10 2.665e-01 -1.083e-09
## log_k1 6.763e-07 1.000e+00 1.112e-04 -2.187e-04 -1.027e-05
## log_k2 -8.944e-10 1.112e-04 1.000e+00 -7.903e-01 9.464e-09
## g_qlogis 2.665e-01 -2.187e-04 -7.903e-01 1.000e+00 -1.532e-08
## sigma -1.083e-09 -1.027e-05 9.464e-09 -1.532e-08 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 93.9500 9.397e+01 2.036e-12 91.5900 96.3100
## k1 22.4900 5.533e-04 4.998e-01 0.0000 Inf
## k2 0.3369 1.591e+01 4.697e-07 0.2904 0.3909
## g 0.4016 1.680e+01 3.238e-07 0.3466 0.4591
## sigma 1.4140 4.899e+00 8.776e-04 0.7314 2.0960
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 2.53 4 2
## parent 2.53 4 2
##
## Estimated disappearance times:
## DT50 DT90 DT50back DT50_k1 DT50_k2
## parent 0.5335 5.311 1.599 0.03083 2.058Here, the DFOP model is clearly the best-fit model for dataset L2 based on the chi^2 error level criterion.
Laboratory Data L3
The following code defines example dataset L3 from the FOCUS kinetics report, p. 290.
FOCUS_2006_L3 = data.frame(
t = c(0, 3, 7, 14, 30, 60, 91, 120),
parent = c(97.8, 60, 51, 43, 35, 22, 15, 12))
FOCUS_2006_L3_mkin <- mkin_wide_to_long(FOCUS_2006_L3)Fit multiple models
As of mkin version 0.9-39 (June 2015), we can fit several models to
one or more datasets in one call to the function mmkin. The
datasets have to be passed in a list, in this case a named list holding
only the L3 dataset prepared above.
# Only use one core here, not to offend the CRAN checks
mm.L3 <- mmkin(c("SFO", "FOMC", "DFOP"), cores = 1,
list("FOCUS L3" = FOCUS_2006_L3_mkin), quiet = TRUE)
plot(mm.L3)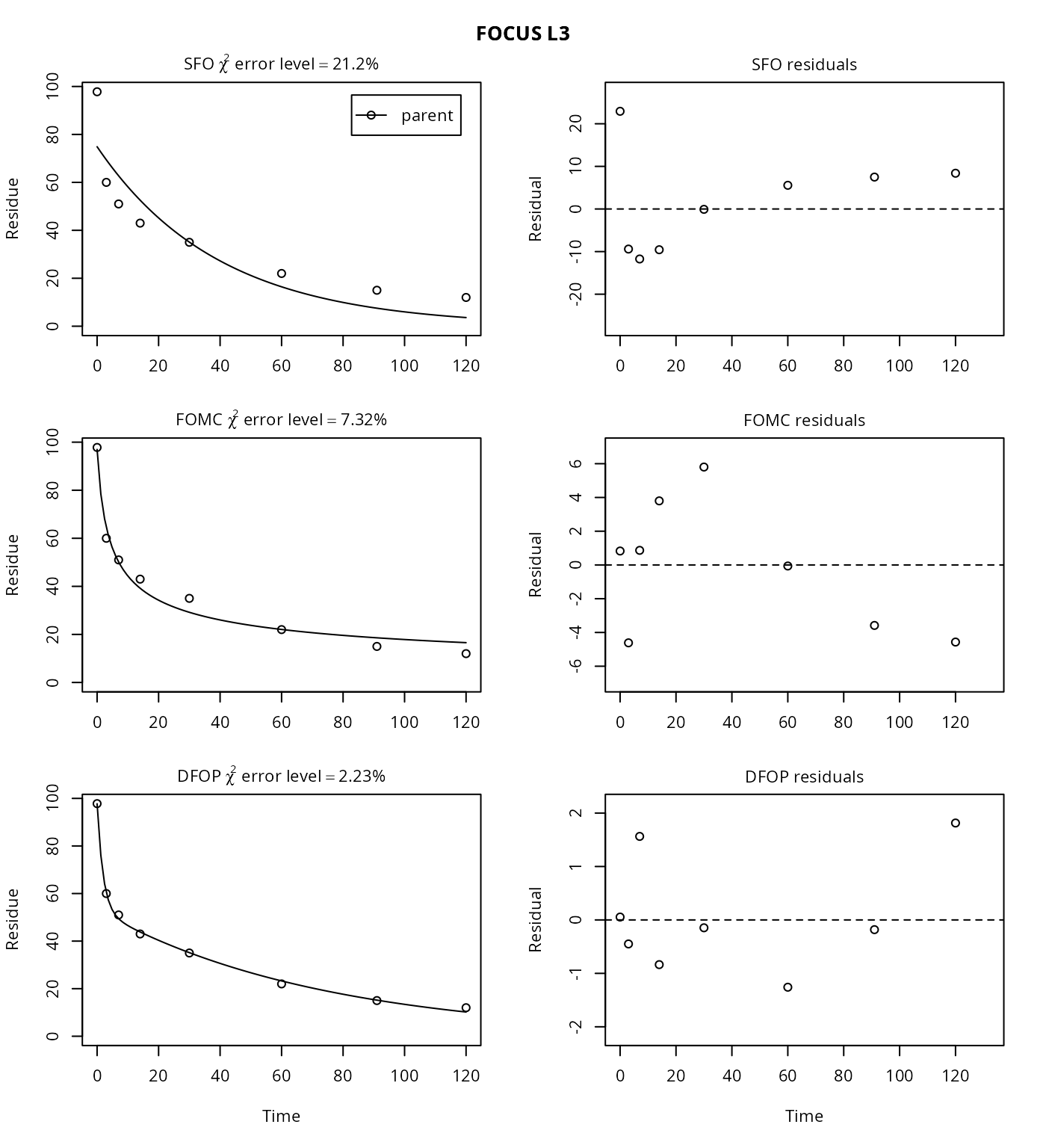
The \(\chi^2\) error level of 21% as well as the plot suggest that the SFO model does not fit very well. The FOMC model performs better, with an error level at which the \(\chi^2\) test passes of 7%. Fitting the four parameter DFOP model further reduces the \(\chi^2\) error level considerably.
Accessing mmkin objects
The objects returned by mmkin are arranged like a matrix, with models as a row index and datasets as a column index.
We can extract the summary and plot for e.g. the DFOP fit, using square brackets for indexing which will result in the use of the summary and plot functions working on mkinfit objects.
summary(mm.L3[["DFOP", 1]])## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:14 2023
## Date of summary: Thu Nov 16 04:20:14 2023
##
## Equations:
## d_parent/dt = - ((k1 * g * exp(-k1 * time) + k2 * (1 - g) * exp(-k2 *
## time)) / (g * exp(-k1 * time) + (1 - g) * exp(-k2 * time)))
## * parent
##
## Model predictions using solution type analytical
##
## Fitted using 376 model solutions performed in 0.024 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 97.80 state
## k1 0.10 deparm
## k2 0.01 deparm
## g 0.50 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 97.800000 -Inf Inf
## log_k1 -2.302585 -Inf Inf
## log_k2 -4.605170 -Inf Inf
## g_qlogis 0.000000 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 32.97732 33.37453 -11.48866
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 97.7500 1.01900 94.5000 101.000000
## log_k1 -0.6612 0.10050 -0.9812 -0.341300
## log_k2 -4.2860 0.04322 -4.4230 -4.148000
## g_qlogis -0.1739 0.05270 -0.3416 -0.006142
## sigma 1.0170 0.25430 0.2079 1.827000
##
## Parameter correlation:
## parent_0 log_k1 log_k2 g_qlogis sigma
## parent_0 1.000e+00 1.732e-01 2.282e-02 4.009e-01 -9.696e-08
## log_k1 1.732e-01 1.000e+00 4.945e-01 -5.809e-01 7.148e-07
## log_k2 2.282e-02 4.945e-01 1.000e+00 -6.812e-01 1.022e-06
## g_qlogis 4.009e-01 -5.809e-01 -6.812e-01 1.000e+00 -7.930e-07
## sigma -9.696e-08 7.148e-07 1.022e-06 -7.930e-07 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 97.75000 95.960 1.248e-06 94.50000 101.00000
## k1 0.51620 9.947 1.081e-03 0.37490 0.71090
## k2 0.01376 23.140 8.840e-05 0.01199 0.01579
## g 0.45660 34.920 2.581e-05 0.41540 0.49850
## sigma 1.01700 4.000 1.400e-02 0.20790 1.82700
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 2.225 4 4
## parent 2.225 4 4
##
## Estimated disappearance times:
## DT50 DT90 DT50back DT50_k1 DT50_k2
## parent 7.464 123 37.03 1.343 50.37
##
## Data:
## time variable observed predicted residual
## 0 parent 97.8 97.75 0.05396
## 3 parent 60.0 60.45 -0.44933
## 7 parent 51.0 49.44 1.56338
## 14 parent 43.0 43.84 -0.83632
## 30 parent 35.0 35.15 -0.14707
## 60 parent 22.0 23.26 -1.25919
## 91 parent 15.0 15.18 -0.18181
## 120 parent 12.0 10.19 1.81395
plot(mm.L3[["DFOP", 1]], show_errmin = TRUE)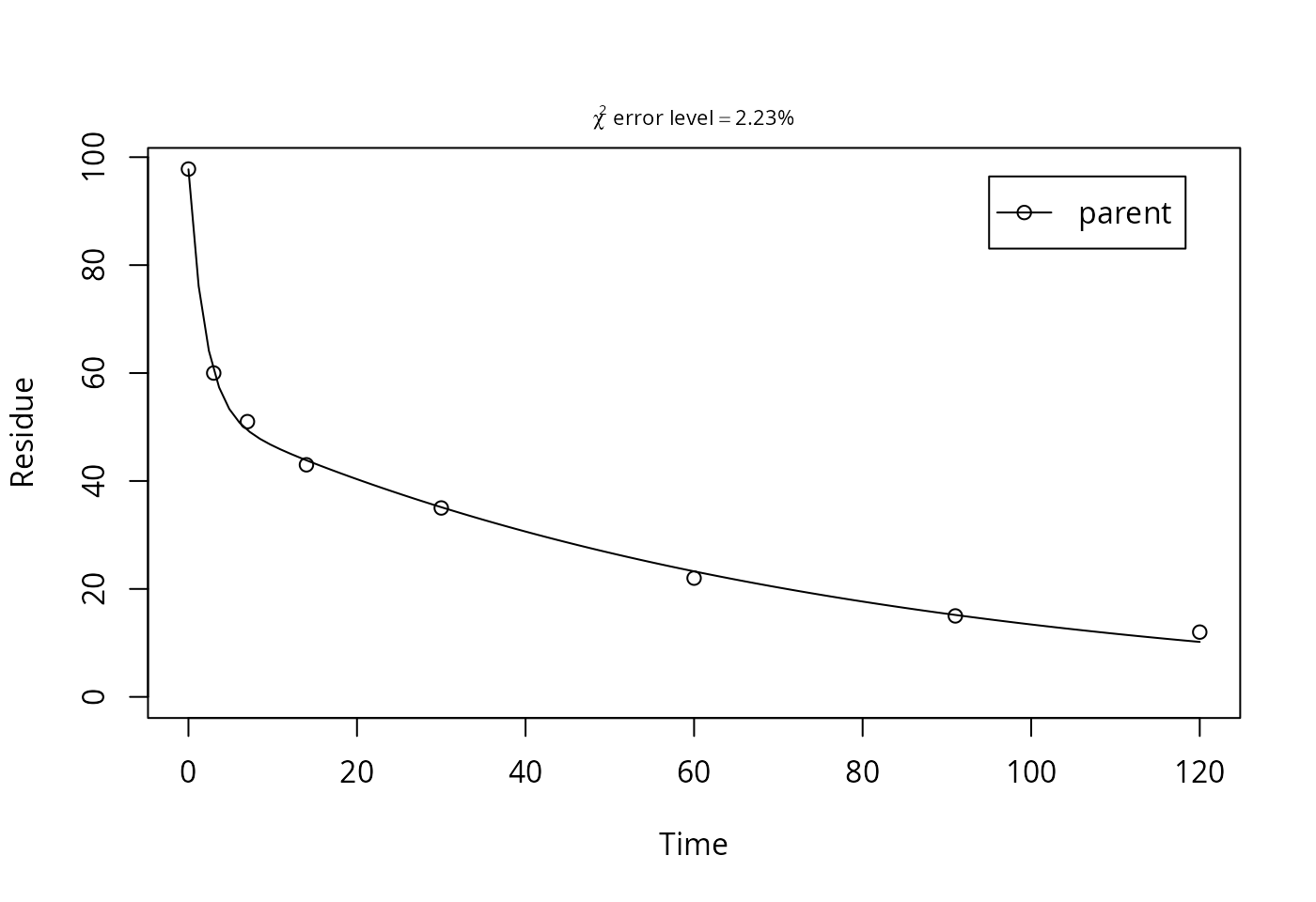
Here, a look to the model plot, the confidence intervals of the parameters and the correlation matrix suggest that the parameter estimates are reliable, and the DFOP model can be used as the best-fit model based on the \(\chi^2\) error level criterion for laboratory data L3.
This is also an example where the standard t-test for the parameter
g_ilr is misleading, as it tests for a significant
difference from zero. In this case, zero appears to be the correct value
for this parameter, and the confidence interval for the backtransformed
parameter g is quite narrow.
Laboratory Data L4
The following code defines example dataset L4 from the FOCUS kinetics report, p. 293:
FOCUS_2006_L4 = data.frame(
t = c(0, 3, 7, 14, 30, 60, 91, 120),
parent = c(96.6, 96.3, 94.3, 88.8, 74.9, 59.9, 53.5, 49.0))
FOCUS_2006_L4_mkin <- mkin_wide_to_long(FOCUS_2006_L4)Fits of the SFO and FOMC models, plots and summaries are produced below:
# Only use one core here, not to offend the CRAN checks
mm.L4 <- mmkin(c("SFO", "FOMC"), cores = 1,
list("FOCUS L4" = FOCUS_2006_L4_mkin),
quiet = TRUE)
plot(mm.L4)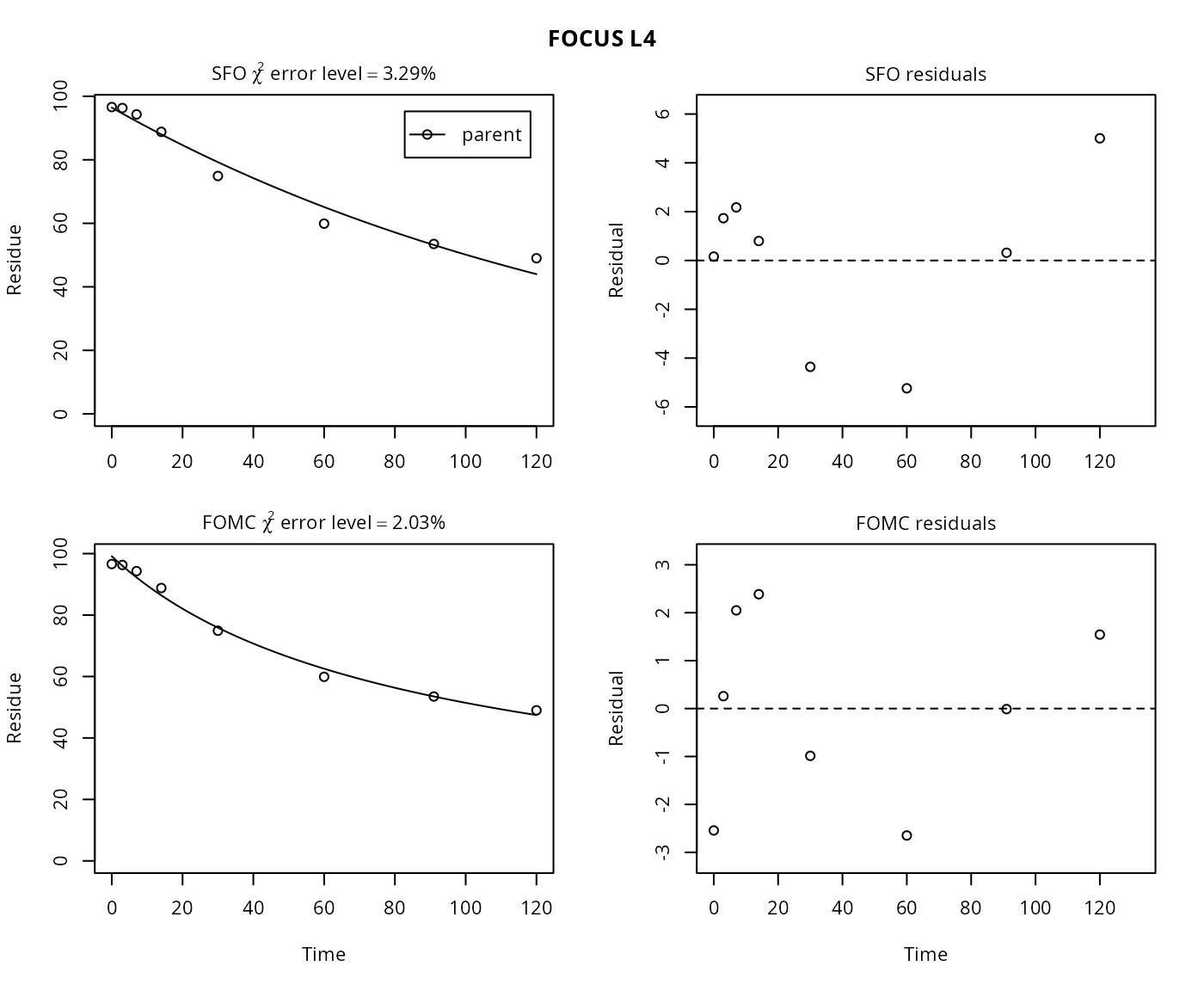
The \(\chi^2\) error level of 3.3% as well as the plot suggest that the SFO model fits very well. The error level at which the \(\chi^2\) test passes is slightly lower for the FOMC model. However, the difference appears negligible.
summary(mm.L4[["SFO", 1]], data = FALSE)## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:14 2023
## Date of summary: Thu Nov 16 04:20:15 2023
##
## Equations:
## d_parent/dt = - k_parent * parent
##
## Model predictions using solution type analytical
##
## Fitted using 142 model solutions performed in 0.01 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 96.6 state
## k_parent 0.1 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 96.600000 -Inf Inf
## log_k_parent -2.302585 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 47.12133 47.35966 -20.56067
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 96.440 1.69900 92.070 100.800
## log_k_parent -5.030 0.07059 -5.211 -4.848
## sigma 3.162 0.79050 1.130 5.194
##
## Parameter correlation:
## parent_0 log_k_parent sigma
## parent_0 1.000e+00 5.938e-01 3.430e-07
## log_k_parent 5.938e-01 1.000e+00 5.885e-07
## sigma 3.430e-07 5.885e-07 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 96.440000 56.77 1.604e-08 92.070000 1.008e+02
## k_parent 0.006541 14.17 1.578e-05 0.005455 7.842e-03
## sigma 3.162000 4.00 5.162e-03 1.130000 5.194e+00
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 3.287 2 6
## parent 3.287 2 6
##
## Estimated disappearance times:
## DT50 DT90
## parent 106 352
summary(mm.L4[["FOMC", 1]], data = FALSE)## mkin version used for fitting: 1.2.6
## R version used for fitting: 4.3.2
## Date of fit: Thu Nov 16 04:20:15 2023
## Date of summary: Thu Nov 16 04:20:15 2023
##
## Equations:
## d_parent/dt = - (alpha/beta) * 1/((time/beta) + 1) * parent
##
## Model predictions using solution type analytical
##
## Fitted using 224 model solutions performed in 0.014 s
##
## Error model: Constant variance
##
## Error model algorithm: OLS
##
## Starting values for parameters to be optimised:
## value type
## parent_0 96.6 state
## alpha 1.0 deparm
## beta 10.0 deparm
##
## Starting values for the transformed parameters actually optimised:
## value lower upper
## parent_0 96.600000 -Inf Inf
## log_alpha 0.000000 -Inf Inf
## log_beta 2.302585 -Inf Inf
##
## Fixed parameter values:
## None
##
## Results:
##
## AIC BIC logLik
## 40.37255 40.69032 -16.18628
##
## Optimised, transformed parameters with symmetric confidence intervals:
## Estimate Std. Error Lower Upper
## parent_0 99.1400 1.2670 95.6300 102.7000
## log_alpha -0.3506 0.2616 -1.0770 0.3756
## log_beta 4.1740 0.3938 3.0810 5.2670
## sigma 1.8300 0.4575 0.5598 3.1000
##
## Parameter correlation:
## parent_0 log_alpha log_beta sigma
## parent_0 1.000e+00 -4.696e-01 -5.543e-01 -2.447e-07
## log_alpha -4.696e-01 1.000e+00 9.889e-01 2.198e-08
## log_beta -5.543e-01 9.889e-01 1.000e+00 4.923e-08
## sigma -2.447e-07 2.198e-08 4.923e-08 1.000e+00
##
## Backtransformed parameters:
## Confidence intervals for internally transformed parameters are asymmetric.
## t-test (unrealistically) based on the assumption of normal distribution
## for estimators of untransformed parameters.
## Estimate t value Pr(>t) Lower Upper
## parent_0 99.1400 78.250 7.993e-08 95.6300 102.700
## alpha 0.7042 3.823 9.365e-03 0.3407 1.456
## beta 64.9800 2.540 3.201e-02 21.7800 193.900
## sigma 1.8300 4.000 8.065e-03 0.5598 3.100
##
## FOCUS Chi2 error levels in percent:
## err.min n.optim df
## All data 2.029 3 5
## parent 2.029 3 5
##
## Estimated disappearance times:
## DT50 DT90 DT50back
## parent 108.9 1644 494.9