Testing hierarchical pathway kinetics with residue data on dimethenamid and dimethenamid-P

Introduction

The purpose of this document is to test demonstrate how nonlinear hierarchical models (NLHM) based on the parent degradation models SFO, FOMC, DFOP and HS, with parallel formation of two or more metabolites can be fitted with the mkin package.

It was assembled in the course of work package 1.2 of Project Number 173340 (Application of nonlinear hierarchical models to the kinetic evaluation of chemical degradation data) of the German Environment Agency carried out in 2022 and 2023.

The mkin package is used in version 1.2.5, which is currently under development. It contains the test data, and the functions used in the evaluations. The saemix package is used as a backend for fitting the NLHM, but is also loaded to make the convergence plot function available.

This document is processed with the knitr package, which also provides the kable function that is used to improve the display of tabular data in R markdown documents. For parallel processing, the parallel package is used.

library(mkin)
library(knitr)
library(saemix)
library(parallel)
n_cores <- detectCores()

# We need to start a new cluster after defining a compiled model that is
# saved as a DLL to the user directory, therefore we define a function
# This is used again after defining the pathway model
start_cluster <- function(n_cores) {
  if (Sys.info()["sysname"] == "Windows") {
    ret <- makePSOCKcluster(n_cores)
  } else {
    ret <- makeForkCluster(n_cores)
  }
  return(ret)
}

Data

The test data are available in the mkin package as an object of class mkindsg (mkin dataset group) under the identifier dimethenamid_2018. The following preprocessing steps are done in this document.

The data available for the enantiomer dimethenamid-P (DMTAP) are renamed to have the same substance name as the data for the racemic mixture dimethenamid (DMTA). The reason for this is that no difference between their degradation behaviour was identified in the EU risk assessment.
Unnecessary columns are discarded
The observation times of each dataset are multiplied with the corresponding normalisation factor also available in the dataset, in order to make it possible to describe all datasets with a single set of parameters that are independent of temperature
Finally, datasets observed in the same soil (Elliot 1 and Elliot 2) are combined, resulting in dimethenamid (DMTA) data from six soils.

The following commented R code performs this preprocessing.

# Apply a function to each of the seven datasets in the mkindsg object to create a list
dmta_ds <- lapply(1:7, function(i) {
  ds_i <- dimethenamid_2018$ds[[i]]$data                     # Get a dataset
  ds_i[ds_i$name == "DMTAP", "name"] <-  "DMTA"              # Rename DMTAP to DMTA
  ds_i <- subset(ds_i, select = c("name", "time", "value")) # Select data
  ds_i$time <- ds_i$time * dimethenamid_2018$f_time_norm[i]  # Normalise time
  ds_i                                                       # Return the dataset
})

# Use dataset titles as names for the list elements
names(dmta_ds) <- sapply(dimethenamid_2018$ds, function(ds) ds$title)

# Combine data for Elliot soil to obtain a named list with six elements
dmta_ds[["Elliot"]] <- rbind(dmta_ds[["Elliot 1"]], dmta_ds[["Elliot 2"]]) #
dmta_ds[["Elliot 1"]] <- NULL
dmta_ds[["Elliot 2"]] <- NULL

The following tables show the 6 datasets.

for (ds_name in names(dmta_ds)) {
  print(
    kable(mkin_long_to_wide(dmta_ds[[ds_name]]),
      caption = paste("Dataset", ds_name),
      booktabs = TRUE, row.names = FALSE))
    cat("\n\\clearpage\n")
}

Dataset Calke
time	DMTA	M23	M27	M31
0	95.8	NA	NA	NA
0	98.7	NA	NA	NA
14	60.5	4.1	1.5	2.0
30	39.1	5.3	2.4	2.1
59	15.2	6.0	3.2	2.2
120	4.8	4.3	3.8	1.8
120	4.6	4.1	3.7	2.1

Dataset Borstel
time	DMTA	M23	M27	M31
0.000000	100.5	NA	NA	NA
0.000000	99.6	NA	NA	NA
1.941295	91.9	0.4	NA	NA
1.941295	91.3	0.5	0.3	0.1
6.794534	81.8	1.2	0.8	1.0
6.794534	82.1	1.3	0.9	0.9
13.589067	69.1	2.8	1.4	2.0
13.589067	68.0	2.0	1.4	2.5
27.178135	51.4	2.9	2.7	4.3
27.178135	51.4	4.9	2.6	3.2
56.297565	27.6	12.2	4.4	4.3
56.297565	26.8	12.2	4.7	4.8
86.387643	15.7	12.2	5.4	5.0
86.387643	15.3	12.0	5.2	5.1
115.507073	7.9	10.4	5.4	4.3
115.507073	8.1	11.6	5.4	4.4

Dataset Flaach
time	DMTA	M23	M27	M31
0.0000000	96.5	NA	NA	NA
0.0000000	96.8	NA	NA	NA
0.0000000	97.0	NA	NA	NA
0.6233856	82.9	0.7	1.1	0.3
0.6233856	86.7	0.7	1.1	0.3
0.6233856	87.4	0.2	0.3	0.1
1.8701567	72.8	2.2	2.6	0.7
1.8701567	69.9	1.8	2.4	0.6
1.8701567	71.9	1.6	2.3	0.7
4.3636989	51.4	4.1	5.0	1.3
4.3636989	52.9	4.2	5.9	1.2
4.3636989	48.6	4.2	4.8	1.4
8.7273979	28.5	7.5	8.5	2.4
8.7273979	27.3	7.1	8.5	2.1
8.7273979	27.5	7.5	8.3	2.3
13.0910968	14.8	8.4	9.3	3.3
13.0910968	13.4	6.8	8.7	2.4
13.0910968	14.4	8.0	9.1	2.6
17.4547957	7.7	7.2	8.6	4.0
17.4547957	7.3	7.2	8.5	3.6
17.4547957	8.1	6.9	8.9	3.3
26.1821936	2.0	4.9	8.1	2.1
26.1821936	1.5	4.3	7.7	1.7
26.1821936	1.9	4.5	7.4	1.8
34.9095915	1.3	3.8	5.9	1.6
34.9095915	1.0	3.1	6.0	1.6
34.9095915	1.1	3.1	5.9	1.4
43.6369893	0.9	2.7	5.6	1.8
43.6369893	0.7	2.3	5.2	1.5
43.6369893	0.7	2.1	5.6	1.3
52.3643872	0.6	1.6	4.3	1.2
52.3643872	0.4	1.1	3.7	0.9
52.3643872	0.5	1.3	3.9	1.1
74.8062674	0.4	0.4	2.5	0.5
74.8062674	0.3	0.4	2.4	0.5
74.8062674	0.3	0.3	2.2	0.3

Dataset BBA 2.2
time	DMTA	M23	M27	M31
0.0000000	98.09	NA	NA	NA
0.0000000	98.77	NA	NA	NA
0.7678922	93.52	0.36	0.42	0.36
0.7678922	92.03	0.40	0.47	0.33
2.3036765	88.39	1.03	0.71	0.55
2.3036765	87.18	1.07	0.82	0.64
5.3752452	69.38	3.60	2.19	1.94
5.3752452	71.06	3.66	2.28	1.62
10.7504904	45.21	6.97	5.45	4.22
10.7504904	46.81	7.22	5.19	4.37
16.1257355	30.54	8.65	8.81	6.31
16.1257355	30.07	8.38	7.93	6.85
21.5009807	21.60	9.10	10.25	7.05
21.5009807	20.41	8.63	10.77	6.84
32.2514711	9.10	7.63	10.89	6.53
32.2514711	9.70	8.01	10.85	7.11
43.0019614	6.58	6.40	10.41	6.06
43.0019614	6.31	6.35	10.35	6.05
53.7524518	3.47	5.35	9.92	5.50
53.7524518	3.52	5.06	9.42	5.07
64.5029421	3.40	5.14	9.15	4.94
64.5029421	3.67	5.91	9.25	4.39
91.3791680	1.62	3.35	7.14	3.64
91.3791680	1.62	2.87	7.13	3.55

Dataset BBA 2.3
time	DMTA	M23	M27	M31
0.0000000	99.33	NA	NA	NA
0.0000000	97.44	NA	NA	NA
0.6733938	93.73	0.18	0.50	0.47
0.6733938	93.77	0.18	0.83	0.34
2.0201814	87.84	0.52	1.25	1.00
2.0201814	89.82	0.43	1.09	0.89
4.7137565	71.61	1.19	3.28	3.58
4.7137565	71.42	1.11	3.24	3.41
9.4275131	45.60	2.26	7.17	8.74
9.4275131	45.42	1.99	7.91	8.28
14.1412696	31.12	2.81	10.15	9.67
14.1412696	31.68	2.83	9.55	8.95
18.8550262	23.20	3.39	12.09	10.34
18.8550262	24.13	3.56	11.89	10.00
28.2825393	9.43	3.49	13.32	7.89
28.2825393	9.82	3.28	12.05	8.13
37.7100523	7.08	2.80	10.04	5.06
37.7100523	8.64	2.97	10.78	5.54
47.1375654	4.41	2.42	9.32	3.79
47.1375654	4.78	2.51	9.62	4.11
56.5650785	4.92	2.22	8.00	3.11
56.5650785	5.08	1.95	8.45	2.98
80.1338612	2.13	1.28	5.71	1.78
80.1338612	2.23	0.99	3.33	1.55

Dataset Elliot
time	DMTA	M23	M27	M31
0.000000	97.5	NA	NA	NA
0.000000	100.7	NA	NA	NA
1.228478	86.4	NA	NA	NA
1.228478	88.5	NA	NA	1.5
3.685435	69.8	2.8	2.3	5.0
3.685435	77.1	1.7	2.1	2.4
8.599349	59.0	4.3	4.0	4.3
8.599349	54.2	5.8	3.4	5.0
17.198697	31.3	8.2	6.6	8.0
17.198697	33.5	5.2	6.9	7.7
25.798046	19.6	5.1	8.2	7.8
25.798046	20.9	6.1	8.8	6.5
34.397395	13.3	6.0	9.7	8.0
34.397395	15.8	6.0	8.8	7.4
51.596092	6.7	5.0	8.3	6.9
51.596092	8.7	4.2	9.2	9.0
68.794789	8.8	3.9	9.3	5.5
68.794789	8.7	2.9	8.5	6.1
103.192184	6.0	1.9	8.6	6.1
103.192184	4.4	1.5	6.0	4.0
146.188928	3.3	2.0	5.6	3.1
146.188928	2.8	2.3	4.5	2.9
223.583066	1.4	1.2	4.1	1.8
223.583066	1.8	1.9	3.9	2.6
0.000000	93.4	NA	NA	NA
0.000000	103.2	NA	NA	NA
1.228478	89.2	NA	NA	1.3
1.228478	86.6	NA	NA	NA
3.685435	78.2	2.6	1.0	3.1
3.685435	78.1	2.4	2.6	2.3
8.599349	55.6	5.5	4.5	3.4
8.599349	53.0	5.6	4.6	4.3
17.198697	33.7	7.3	7.6	7.8
17.198697	33.2	6.5	6.7	8.7
25.798046	20.9	5.8	8.7	7.7
25.798046	19.9	7.7	7.6	6.5
34.397395	18.2	7.8	8.0	6.3
34.397395	12.7	7.3	8.6	8.7
51.596092	7.8	7.0	7.4	5.7
51.596092	9.0	6.3	7.2	4.2
68.794789	11.4	4.3	10.3	3.2
68.794789	9.0	3.8	9.4	4.2
103.192184	3.9	2.6	6.5	3.8
103.192184	4.4	2.8	6.9	4.0
146.188928	2.6	1.6	4.6	4.5
146.188928	3.4	1.1	4.5	4.5
223.583066	2.0	1.4	4.3	3.8
223.583066	1.7	1.3	4.2	2.3

Separate evaluations

As a first step to obtain suitable starting parameters for the NLHM fits, we do separate fits of several variants of the pathway model used previously (Ranke et al. 2021), varying the kinetic model for the parent compound. Because the SFORB model often provides faster convergence than the DFOP model, and can sometimes be fitted where the DFOP model results in errors, it is included in the set of parent models tested here.

if (!dir.exists("dmta_dlls")) dir.create("dmta_dlls")
m_sfo_path_1 <- mkinmod(
  DMTA = mkinsub("SFO", c("M23", "M27", "M31")),
  M23 = mkinsub("SFO"),
  M27 = mkinsub("SFO"),
  M31 = mkinsub("SFO", "M27", sink = FALSE),
  name = "m_sfo_path", dll_dir = "dmta_dlls",
  unload = TRUE, overwrite = TRUE,
  quiet = TRUE
)
m_fomc_path_1 <- mkinmod(
  DMTA = mkinsub("FOMC", c("M23", "M27", "M31")),
  M23 = mkinsub("SFO"),
  M27 = mkinsub("SFO"),
  M31 = mkinsub("SFO", "M27", sink = FALSE),
  name = "m_fomc_path", dll_dir = "dmta_dlls",
  unload = TRUE, overwrite = TRUE,
  quiet = TRUE
)
m_dfop_path_1 <- mkinmod(
  DMTA = mkinsub("DFOP", c("M23", "M27", "M31")),
  M23 = mkinsub("SFO"),
  M27 = mkinsub("SFO"),
  M31 = mkinsub("SFO", "M27", sink = FALSE),
  name = "m_dfop_path", dll_dir = "dmta_dlls",
  unload = TRUE, overwrite = TRUE,
  quiet = TRUE
)
m_sforb_path_1 <- mkinmod(
  DMTA = mkinsub("SFORB", c("M23", "M27", "M31")),
  M23 = mkinsub("SFO"),
  M27 = mkinsub("SFO"),
  M31 = mkinsub("SFO", "M27", sink = FALSE),
  name = "m_sforb_path", dll_dir = "dmta_dlls",
  unload = TRUE, overwrite = TRUE,
  quiet = TRUE
)
m_hs_path_1 <- mkinmod(
  DMTA = mkinsub("HS", c("M23", "M27", "M31")),
  M23 = mkinsub("SFO"),
  M27 = mkinsub("SFO"),
  M31 = mkinsub("SFO", "M27", sink = FALSE),
  name = "m_hs_path", dll_dir = "dmta_dlls",
  unload = TRUE, overwrite = TRUE,
  quiet = TRUE
)
cl <- start_cluster(n_cores)

deg_mods_1 <- list(
  sfo_path_1 = m_sfo_path_1,
  fomc_path_1 = m_fomc_path_1,
  dfop_path_1 = m_dfop_path_1,
  sforb_path_1 = m_sforb_path_1,
  hs_path_1 = m_hs_path_1)

sep_1_const <- mmkin(
  deg_mods_1,
  dmta_ds,
  error_model = "const",
  quiet = TRUE)

status(sep_1_const) |> kable()

	Calke	Borstel	Flaach	BBA 2.2	BBA 2.3	Elliot
sfo_path_1	OK	OK	OK	OK	OK	OK
fomc_path_1	OK	OK	OK	OK	OK	OK
dfop_path_1	OK	OK	C	OK	OK	OK
sforb_path_1	OK	OK	C	OK	OK	OK
hs_path_1	C	C	C	C	C	C

All separate pathway fits with SFO or FOMC for the parent and constant variance converged (status OK). Most fits with DFOP or SFORB for the parent converged as well. The fits with HS for the parent did not converge with default settings.

sep_1_tc <- update(sep_1_const, error_model = "tc")
status(sep_1_tc) |> kable()

	Calke	Borstel	Flaach	BBA 2.2	BBA 2.3	Elliot
sfo_path_1	OK	OK	OK	OK	OK	OK
fomc_path_1	OK	OK	C	OK	OK	C
dfop_path_1	OK	C	OK	OK	OK	OK
sforb_path_1	OK	C	OK	OK	OK	OK
hs_path_1	C	C	C	C	C	OK

With the two-component error model, the set of fits with convergence problems is slightly different, with convergence problems appearing for different data sets when applying the DFOP and SFORB model and some additional convergence problems when using the FOMC model for the parent.

Hierarchichal model fits

The following code fits two sets of the corresponding hierarchical models to the data, one assuming constant variance, and one assuming two-component error.

saem_1 <- mhmkin(list(sep_1_const, sep_1_tc))

The run time for these fits was around two hours on five year old hardware. After a recent hardware upgrade these fits complete in less than twenty minutes.

status(saem_1) |> kable()

	const	tc
sfo_path_1	OK	OK
fomc_path_1	OK	OK
dfop_path_1	OK	OK
sforb_path_1	OK	OK
hs_path_1	OK	OK

According to the status function, all fits terminated successfully.

anova(saem_1) |> kable(digits = 1)

Warning in FUN(X[[i]], ...): Could not obtain log likelihood with 'is' method
for sforb_path_1 const

	npar	AIC	BIC	Lik
sfo_path_1 const	17	2291.8	2288.3	-1128.9
sfo_path_1 tc	18	2276.3	2272.5	-1120.1
fomc_path_1 const	19	2099.0	2095.0	-1030.5
fomc_path_1 tc	20	1939.6	1935.5	-949.8
dfop_path_1 const	21	2038.8	2034.4	-998.4
hs_path_1 const	21	2024.2	2019.8	-991.1
dfop_path_1 tc	22	1879.8	1875.2	-917.9
sforb_path_1 tc	22	1832.9	1828.3	-894.4
hs_path_1 tc	22	1831.4	1826.8	-893.7

When the goodness-of-fit of the models is compared, a warning is obtained, indicating that the likelihood of the pathway fit with SFORB for the parent compound and constant variance could not be calculated with importance sampling (method ‘is’). As this is the default method on which all AIC and BIC comparisons are based, this variant is not included in the model comparison table. Comparing the goodness-of-fit of the remaining models, HS model model with two-component error provides the best fit. However, for batch experiments performed with constant conditions such as the experiments evaluated here, there is no reason to assume a discontinuity, so the SFORB model is preferable from a mechanistic viewpoint. In addition, the information criteria AIC and BIC are very similar for HS and SFORB. Therefore, the SFORB model is selected here for further refinements.

Parameter identifiability based on the Fisher Information Matrix

Using the illparms function, ill-defined statistical model parameters such as standard deviations of the degradation parameters in the population and error model parameters can be found.

illparms(saem_1) |> kable()

	const	tc
sfo_path_1		sd(DMTA_0)
fomc_path_1		sd(DMTA_0)
dfop_path_1
sforb_path_1		sd(log_k_DMTA_bound_free)
hs_path_1		sd(log_tb)

When using constant variance, no ill-defined variance parameters are identified with the illparms function in any of the degradation models. When using the two-component error model, there is one ill-defined variance parameter in all variants except for the variant using DFOP for the parent compound.

For the selected combination of the SFORB pathway model with two-component error, the random effect for the rate constant from reversibly bound DMTA to the free DMTA (k_DMTA_bound_free) is not well-defined. Therefore, the fit is updated without assuming a random effect for this parameter.

saem_sforb_path_1_tc_reduced <- update(saem_1[["sforb_path_1", "tc"]],
  no_random_effect = "log_k_DMTA_bound_free")
illparms(saem_sforb_path_1_tc_reduced)

As expected, no ill-defined parameters remain. The model comparison below shows that the reduced model is preferable.

anova(saem_1[["sforb_path_1", "tc"]], saem_sforb_path_1_tc_reduced) |> kable(digits = 1)

	npar	AIC	BIC	Lik
saem_sforb_path_1_tc_reduced	21	1830.3	1825.9	-894.2
saem_1[[“sforb_path_1”, “tc”]]	22	1832.9	1828.3	-894.4

The convergence plot of the refined fit is shown below.

plot(saem_sforb_path_1_tc_reduced$so, plot.type = "convergence")

For some parameters, for example for f_DMTA_ilr_1 and f_DMTA_ilr_2, i.e. for two of the parameters determining the formation fractions of the parallel formation of the three metabolites, some movement of the parameters is still visible in the second phase of the algorithm. However, the amplitude of this movement is in the range of the amplitude towards the end of the first phase. Therefore, it is likely that an increase in iterations would not improve the parameter estimates very much, and it is proposed that the fit is acceptable. No numeric convergence criterion is implemented in saemix.

Alternative check of parameter identifiability

As an alternative check of parameter identifiability (Duchesne et al. 2021), multistart runs were performed on the basis of the refined fit shown above.

saem_sforb_path_1_tc_reduced_multi <- multistart(saem_sforb_path_1_tc_reduced,
  n = 32, cores = 10)

print(saem_sforb_path_1_tc_reduced_multi)

<multistart> object with 32 fits:
 E OK 
15 17 
OK: Fit terminated successfully
E: Error

Out of the 32 fits that were initiated, only 17 terminated without an error. The reason for this is that the wide variation of starting parameters in combination with the parameter variation that is used in the SAEM algorithm leads to parameter combinations for the degradation model that the numerical integration routine cannot cope with. Because of this variation of initial parameters, some of the model fits take up to two times more time than the original fit.

par(mar = c(12.1, 4.1, 2.1, 2.1))
parplot(saem_sforb_path_1_tc_reduced_multi, ylim = c(0.5, 2), las = 2)

Parameter boxplots for the multistart runs that succeeded

However, visual analysis of the boxplot of the parameters obtained in the successful fits confirms that the results are sufficiently independent of the starting parameters, and there are no remaining ill-defined parameters.

Plots of selected fits

The SFORB pathway fits with full and reduced parameter distribution model are shown below.

plot(saem_1[["sforb_path_1", "tc"]])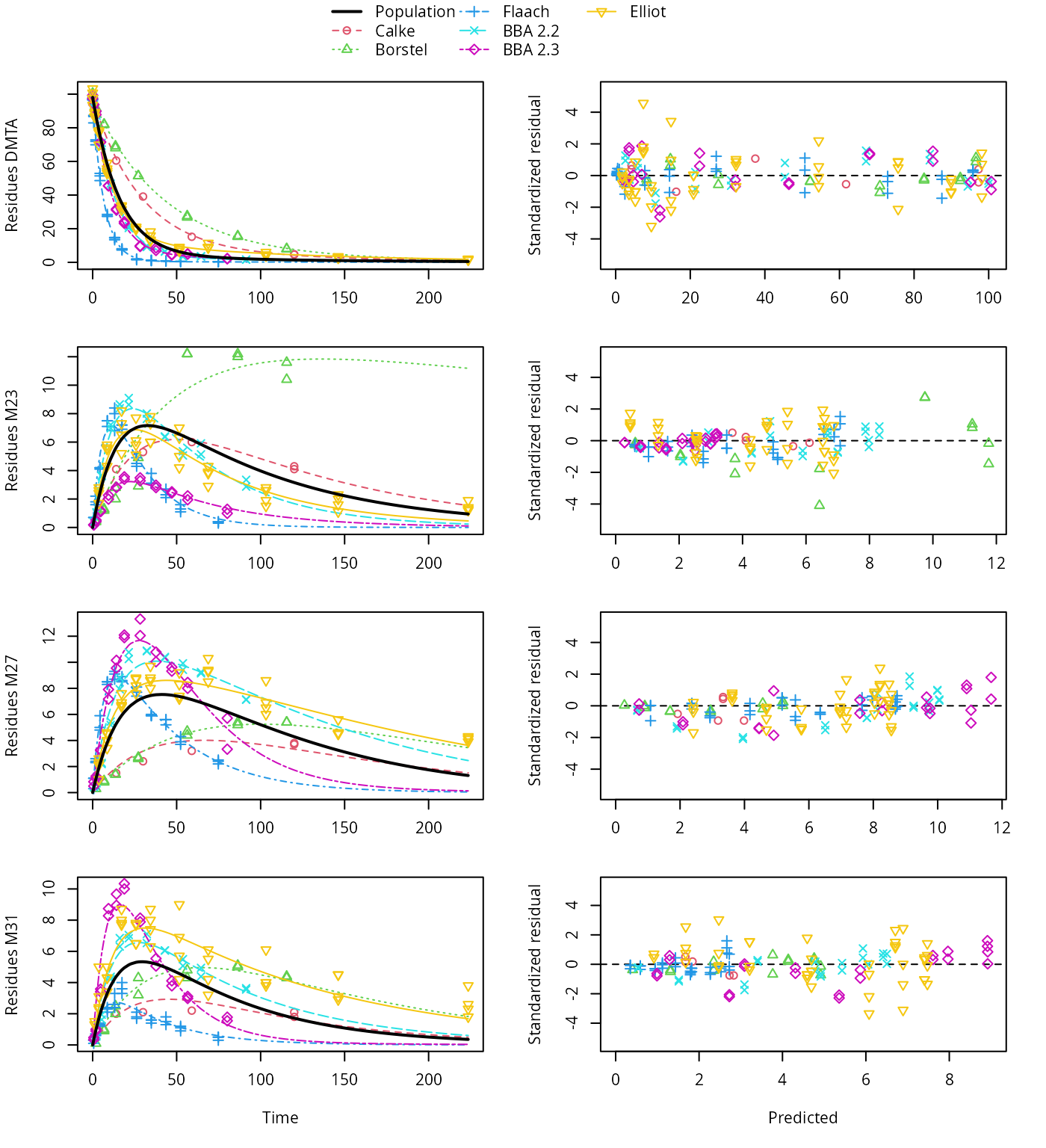

SFORB pathway fit with two-component error

plot(saem_sforb_path_1_tc_reduced)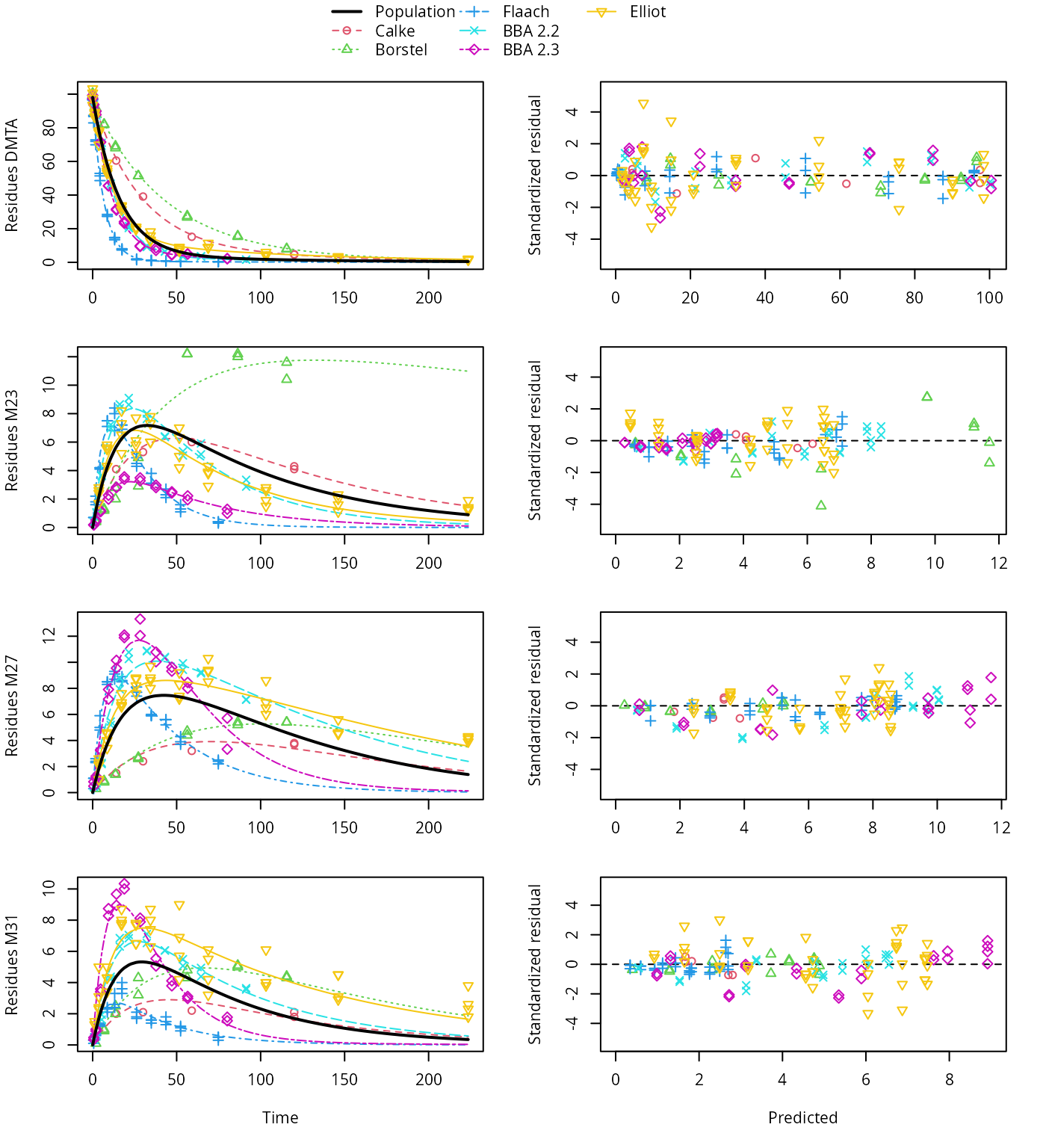

SFORB pathway fit with two-component error, reduced parameter model

Plots of the remaining fits and listings for all successful fits are shown in the Appendix.

stopCluster(cl)

Conclusions

Pathway fits with SFO, FOMC, DFOP, SFORB and HS models for the parent compound could be successfully performed.

Acknowledgements

The helpful comments by Janina Wöltjen of the German Environment Agency on earlier versions of this document are gratefully acknowledged.

References

Duchesne, Ronan, Anissa Guillemin, Olivier Gandrillon, and Fabien Crauste. 2021. “Practical Identifiability in the Frame of Nonlinear Mixed Effects Models: The Example of the in Vitro Erythropoiesis.” BMC Bioinformatics 22 (478). https://doi.org/10.1186/s12859-021-04373-4.

Ranke, Johannes, Janina Wöltjen, Jana Schmidt, and Emmanuelle Comets. 2021. “Taking Kinetic Evaluations of Degradation Data to the Next Level with Nonlinear Mixed-Effects Models.” Environments 8 (8). https://doi.org/10.3390/environments8080071.

Appendix

plot(saem_1[["sfo_path_1", "tc"]])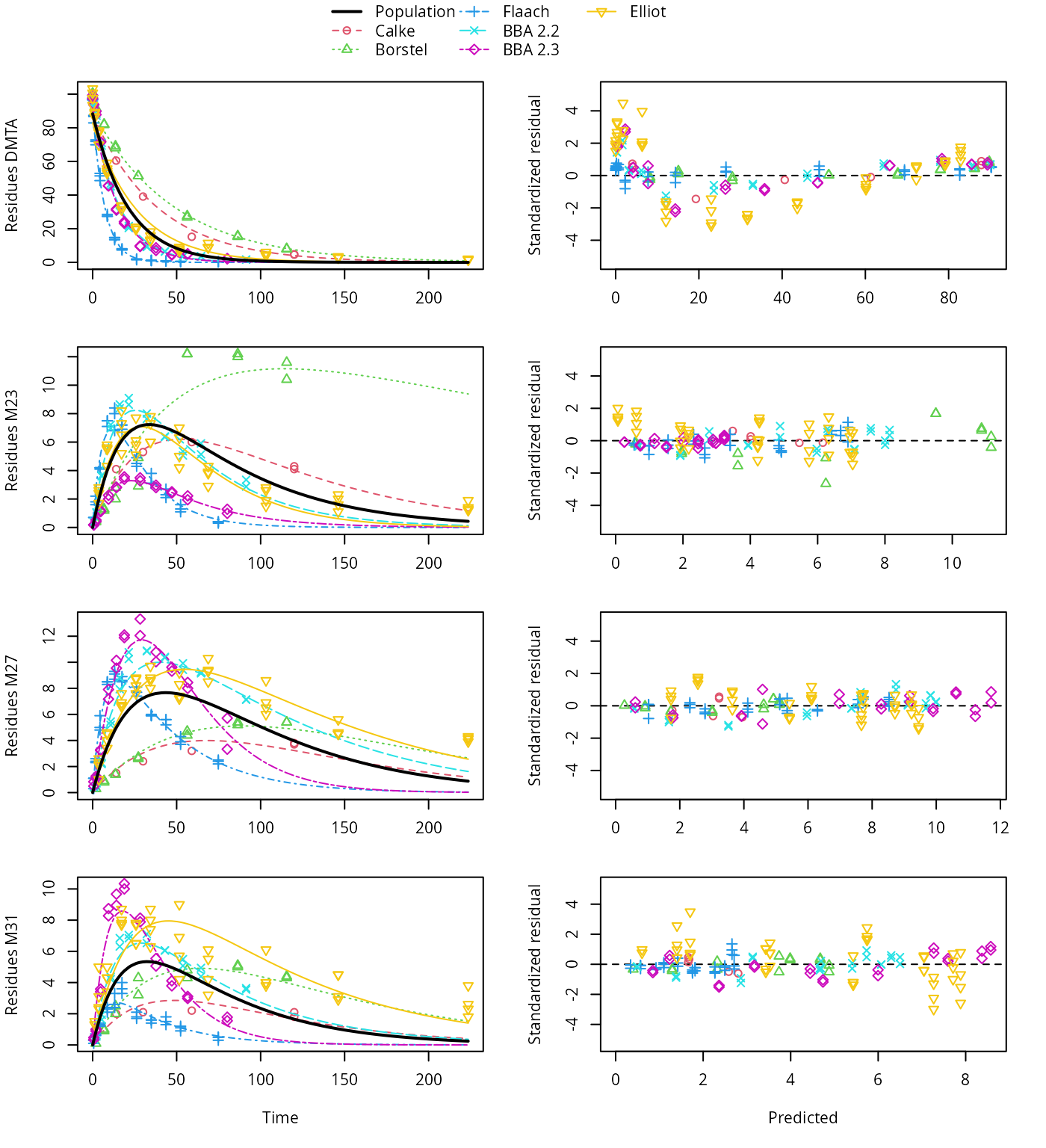

SFO pathway fit with two-component error

plot(saem_1[["fomc_path_1", "tc"]])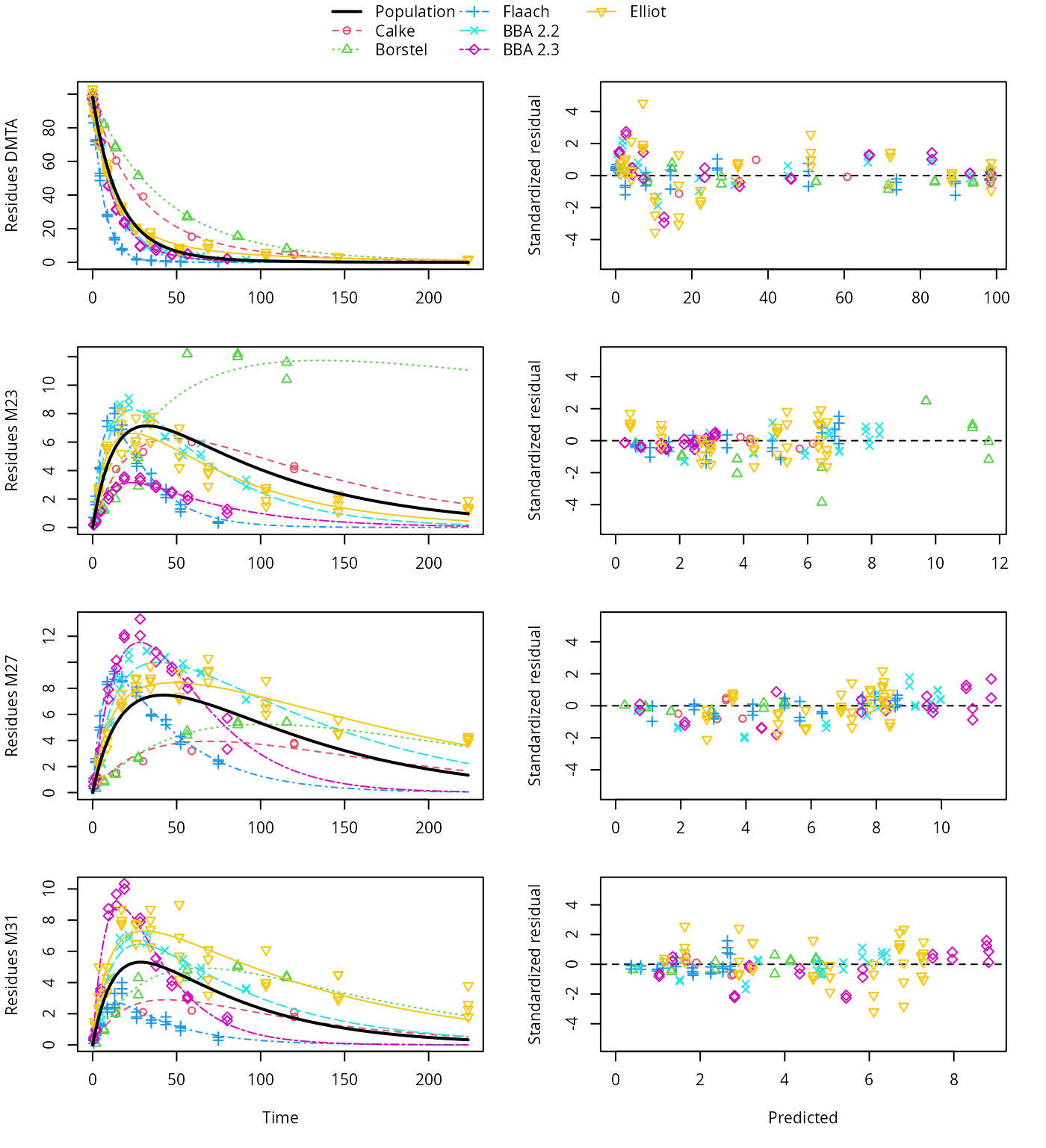

FOMC pathway fit with two-component error

plot(saem_1[["sforb_path_1", "tc"]])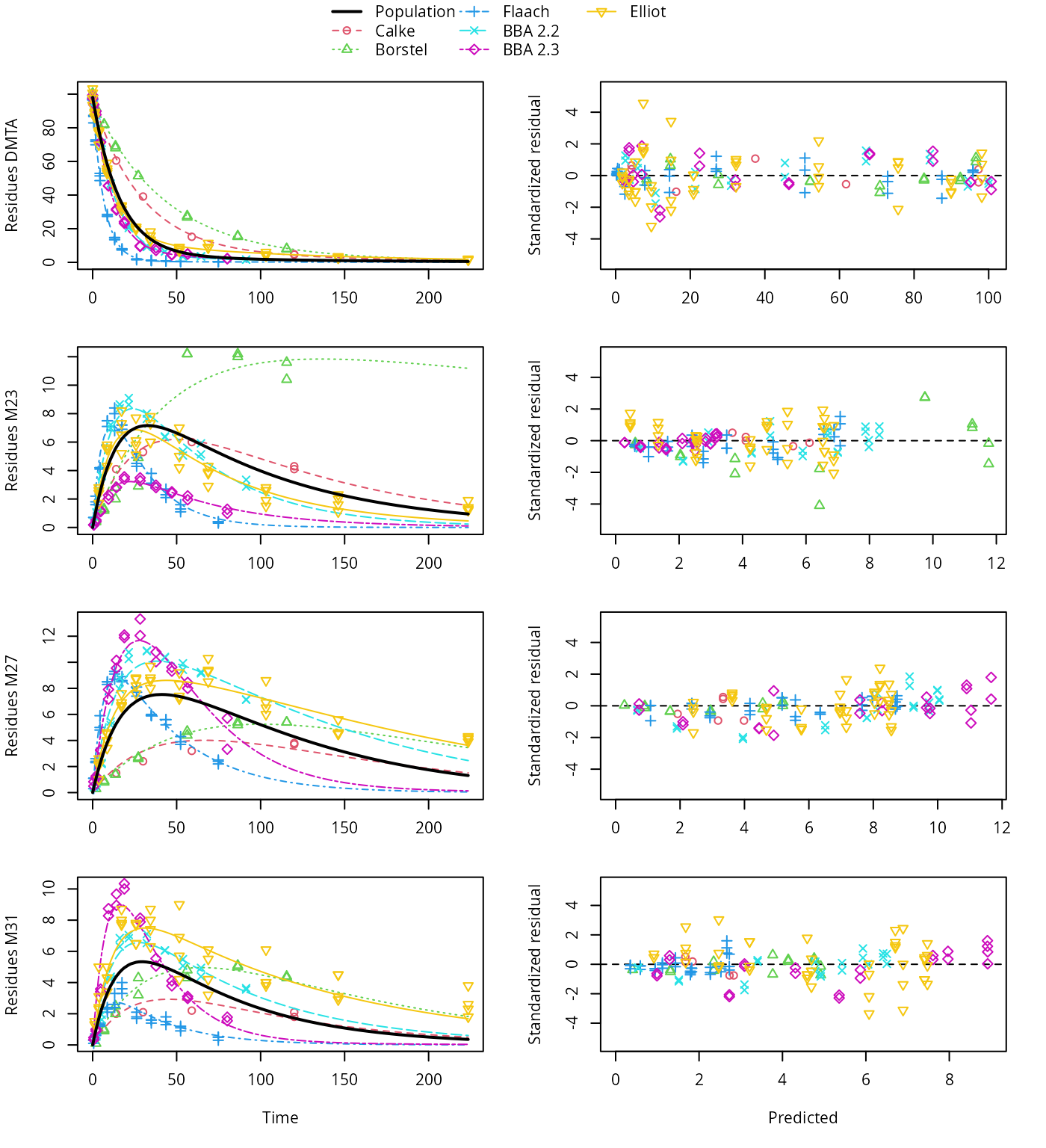

HS pathway fit with two-component error

Hierarchical model fit listings

Fits with random effects for all degradation parameters

Improved fit of the SFORB pathway model with two-component error

Session info

R version 4.3.0 (2023-04-21)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Debian GNU/Linux 12 (bookworm)

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/openblas-serial/libblas.so.3 
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-serial/libopenblas-r0.3.21.so;  LAPACK version 3.11.0

locale:
 [1] LC_CTYPE=de_DE.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=de_DE.UTF-8        LC_COLLATE=de_DE.UTF-8    
 [5] LC_MONETARY=de_DE.UTF-8    LC_MESSAGES=de_DE.UTF-8   
 [7] LC_PAPER=de_DE.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=de_DE.UTF-8 LC_IDENTIFICATION=C       

time zone: Europe/Berlin
tzcode source: system (glibc)

attached base packages:
[1] parallel  stats     graphics  grDevices utils     datasets  methods  
[8] base     

other attached packages:
[1] saemix_3.2 npde_3.3   knitr_1.42 mkin_1.2.5

loaded via a namespace (and not attached):
 [1] sass_0.4.6        utf8_1.2.3        generics_0.1.3    stringi_1.7.12   
 [5] lattice_0.21-8    digest_0.6.31     magrittr_2.0.3    evaluate_0.21    
 [9] grid_4.3.0        fastmap_1.1.1     rprojroot_2.0.3   jsonlite_1.8.4   
[13] processx_3.8.1    pkgbuild_1.4.0    deSolve_1.35      DBI_1.1.3        
[17] mclust_6.0.0      ps_1.7.5          gridExtra_2.3     purrr_1.0.1      
[21] fansi_1.0.4       scales_1.2.1      codetools_0.2-19  textshaping_0.3.6
[25] jquerylib_0.1.4   cli_3.6.1         crayon_1.5.2      rlang_1.1.1      
[29] munsell_0.5.0     cachem_1.0.8      yaml_2.3.7        inline_0.3.19    
[33] tools_4.3.0       memoise_2.0.1     dplyr_1.1.2       colorspace_2.1-0 
[37] ggplot2_3.4.2     vctrs_0.6.2       R6_2.5.1          zoo_1.8-12       
[41] lifecycle_1.0.3   stringr_1.5.0     fs_1.6.2          ragg_1.2.5       
[45] callr_3.7.3       pkgconfig_2.0.3   desc_1.4.2        pkgdown_2.0.7    
[49] bslib_0.4.2       pillar_1.9.0      gtable_0.3.3      glue_1.6.2       
[53] systemfonts_1.0.4 highr_0.10        xfun_0.39         tibble_3.2.1     
[57] lmtest_0.9-40     tidyselect_1.2.0  htmltools_0.5.5   nlme_3.1-162     
[61] rmarkdown_2.21    compiler_4.3.0    prettyunits_1.1.1

Hardware info

CPU model: AMD Ryzen 9 7950X 16-Core Processor

MemTotal:       64925476 kB

Johannes Ranke

Last change on 20 April 2023, last compiled on 19 Mai 2023