This function uses saemix::saemix() as a backend for fitting nonlinear mixed
effects models created from mmkin row objects using the Stochastic Approximation
Expectation Maximisation algorithm (SAEM).
saem(object, control, ...) # S3 method for mmkin saem( object, control = list(displayProgress = FALSE, print = FALSE, save = FALSE, save.graphs = FALSE), cores = 1, verbose = FALSE, suppressPlot = TRUE, quiet = FALSE, ... ) # S3 method for saem.mmkin print(x, digits = max(3, getOption("digits") - 3), ...) saemix_model(object, cores = 1, verbose = FALSE, ...) saemix_data(object, verbose = FALSE, ...)
Arguments
| object | An mmkin row object containing several fits of the same mkinmod model to different datasets |
|---|---|
| control | Passed to saemix::saemix |
| ... | Further parameters passed to saemix::saemixModel. |
| cores | The number of cores to be used for multicore processing using
|
| verbose | Should we print information about created objects of type saemix::SaemixModel and saemix::SaemixData? |
| suppressPlot | Should we suppress any plotting that is done by the saemix function? |
| quiet | Should we suppress the messages saemix prints at the beginning and the end of the optimisation process? |
| x | An saem.mmkin object to print |
| digits | Number of digits to use for printing |
Value
An S3 object of class 'saem.mmkin', containing the fitted saemix::SaemixObject as a list component named 'so'. The object also inherits from 'mixed.mmkin'.
An saemix::SaemixModel object.
An saemix::SaemixData object.
Details
An mmkin row object is essentially a list of mkinfit objects that have been obtained by fitting the same model to a list of datasets using mkinfit.
Starting values for the fixed effects (population mean parameters, argument
psi0 of saemix::saemixModel() are the mean values of the parameters found
using mmkin.
See also
Examples
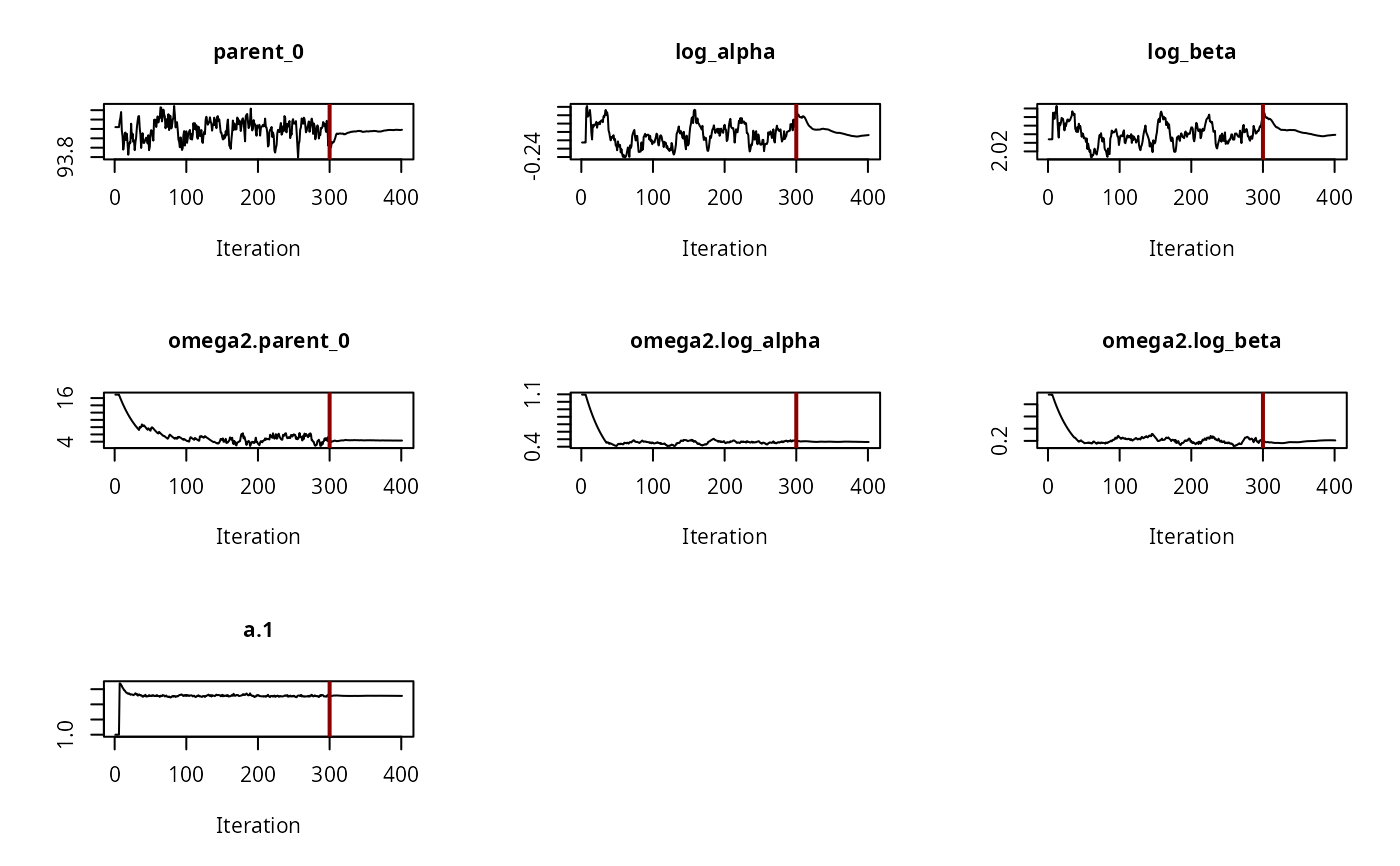
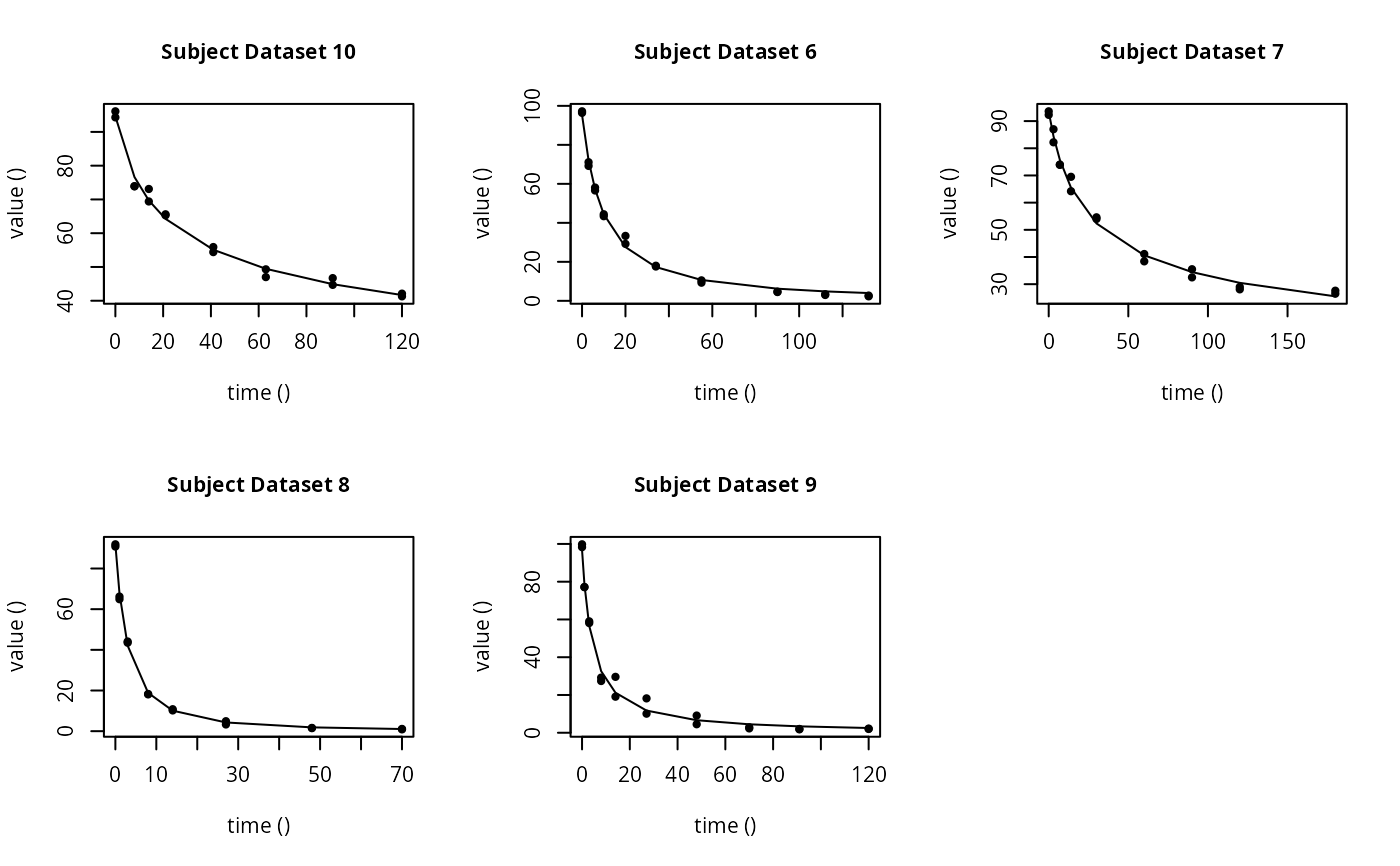
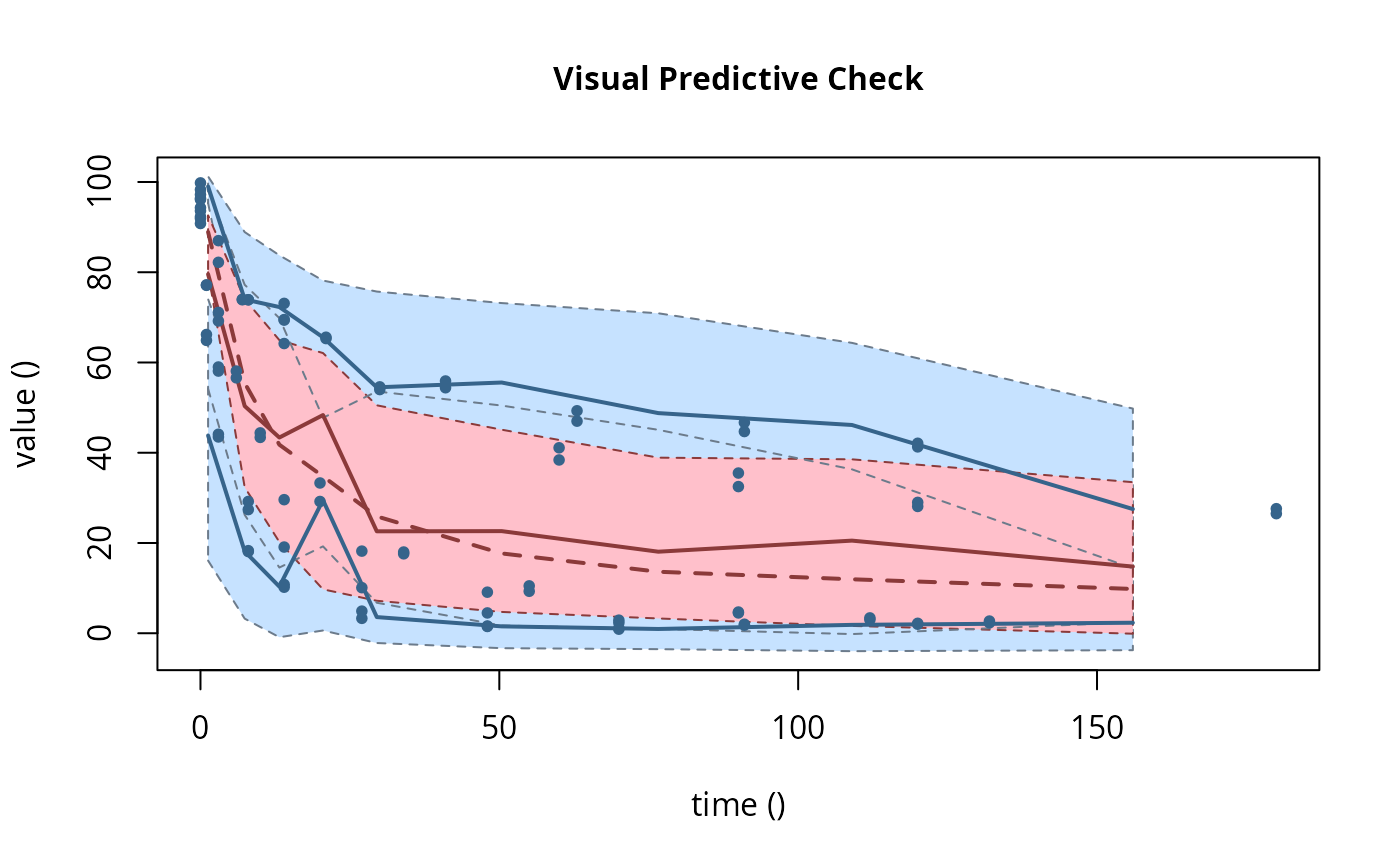
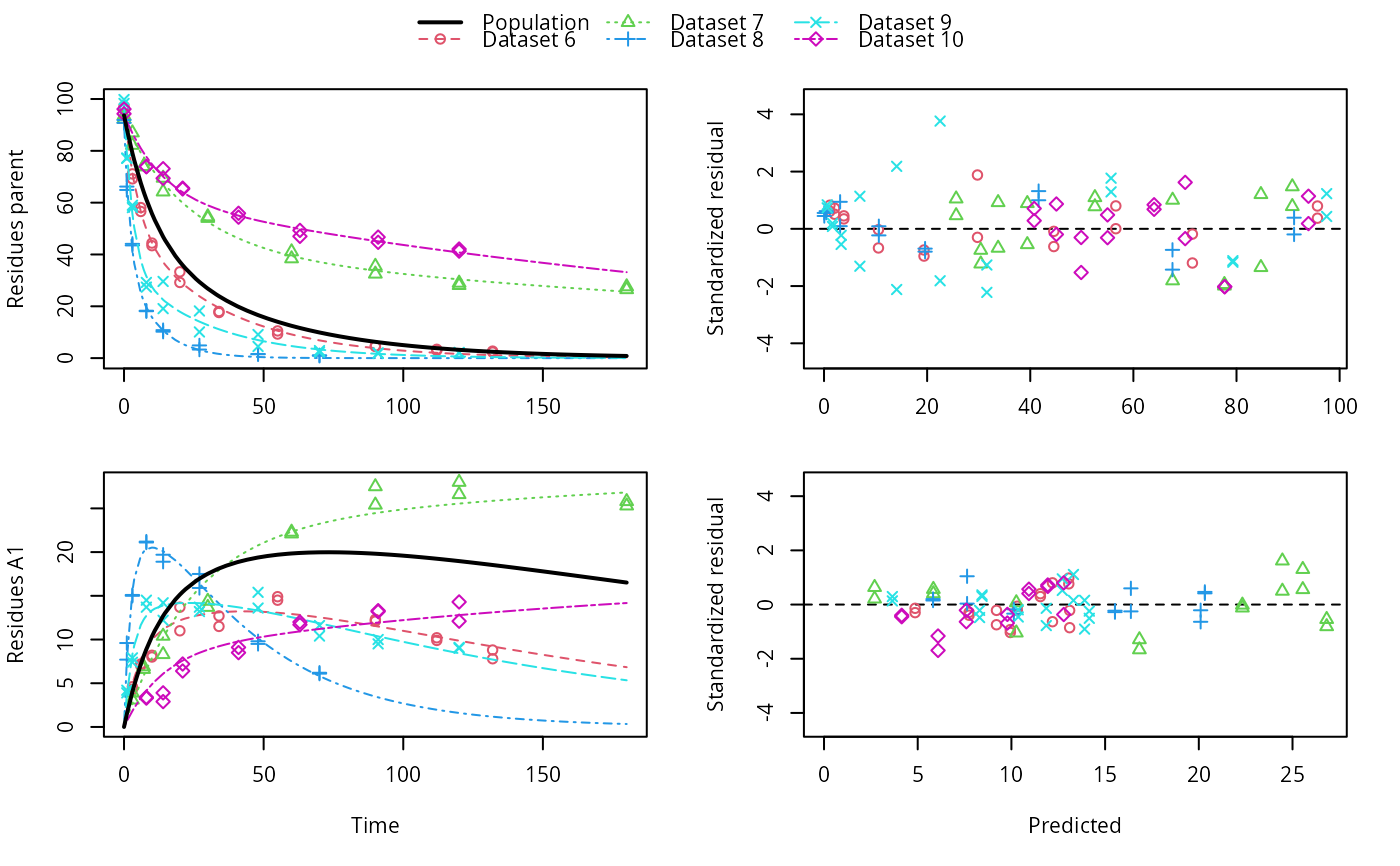
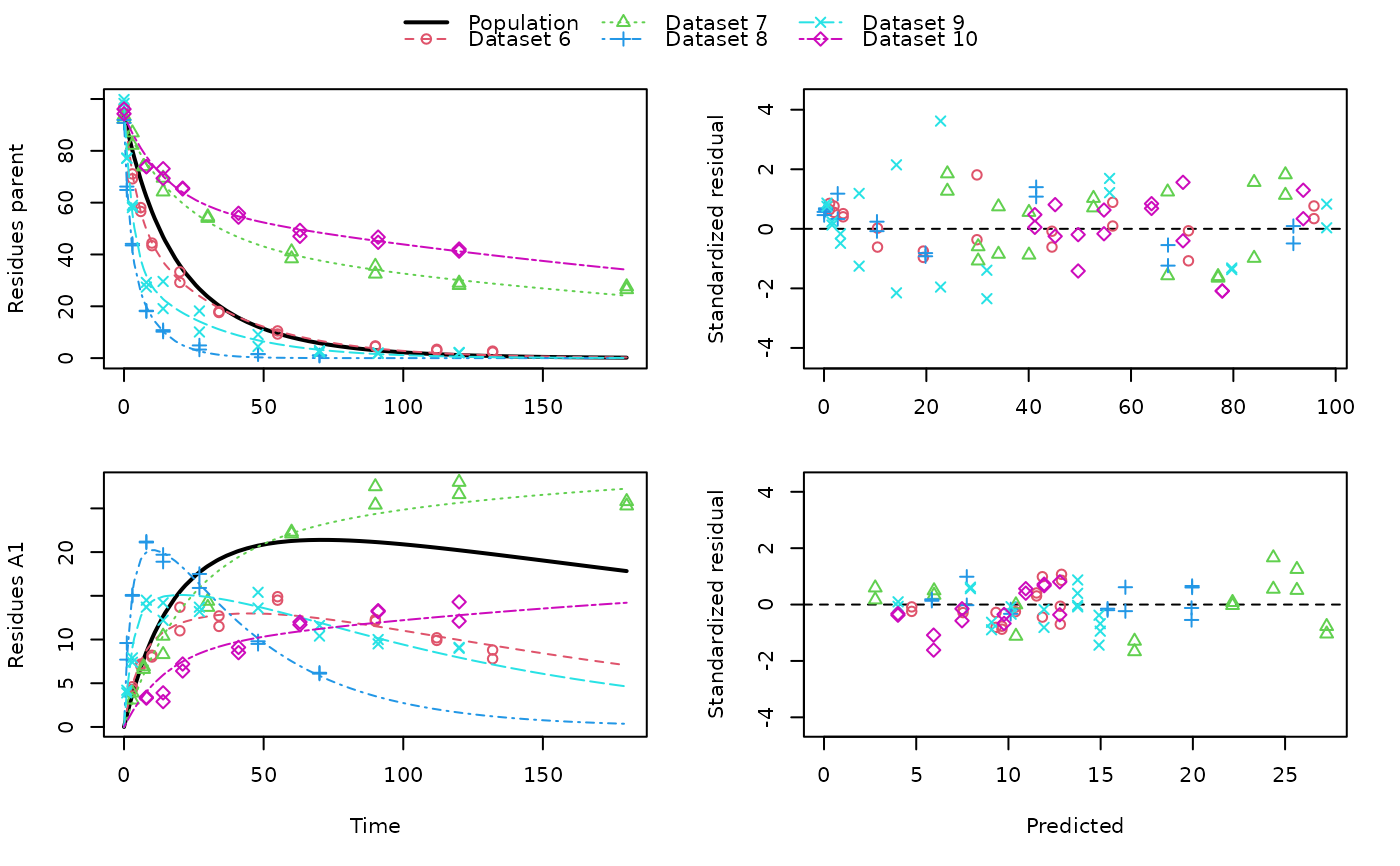
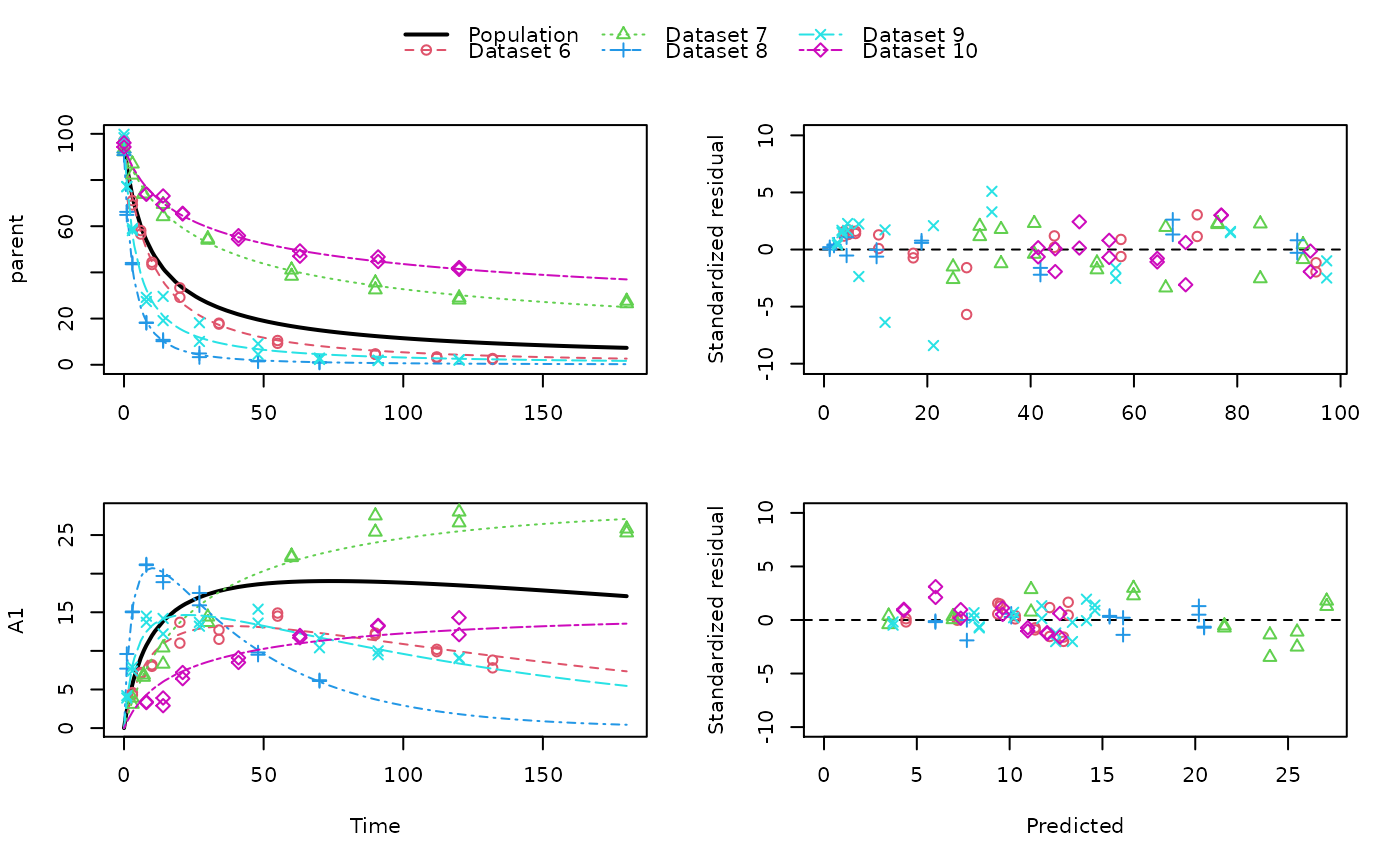
# \dontrun{ ds <- lapply(experimental_data_for_UBA_2019[6:10], function(x) subset(x$data[c("name", "time", "value")])) names(ds) <- paste("Dataset", 6:10) f_mmkin_parent_p0_fixed <- mmkin("FOMC", ds, cores = 1, state.ini = c(parent = 100), fixed_initials = "parent", quiet = TRUE) f_saem_p0_fixed <- saem(f_mmkin_parent_p0_fixed)#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:02 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:04 2020"f_mmkin_parent <- mmkin(c("SFO", "FOMC", "DFOP"), ds, quiet = TRUE) f_saem_sfo <- saem(f_mmkin_parent["SFO", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:05 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:07 2020"f_saem_fomc <- saem(f_mmkin_parent["FOMC", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:07 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:09 2020"f_saem_dfop <- saem(f_mmkin_parent["DFOP", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:10 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:13 2020"# The returned saem.mmkin object contains an SaemixObject, therefore we can use # functions from saemix library(saemix)#> #>#> Likelihoods computed by importance sampling#> AIC BIC #> 1 624.2484 622.2956 #> 2 467.7096 464.9757 #> 3 495.4373 491.9222#> Plotting convergence plots#> Plotting individual fits#> Simulating data using nsim = 1000 simulated datasets #> Computing WRES and npde . #> Plotting npde#> --------------------------------------------- #> Distribution of npde: #> mean= -0.01528 (SE= 0.098 ) #> variance= 0.862 (SE= 0.13 ) #> skewness= 0.5016 #> kurtosis= 1.18 #> --------------------------------------------- #> #> Statistical tests #> Wilcoxon signed rank test : 0.679 #> Fisher variance test : 0.36 #> SW test of normality : 0.0855 . #> Global adjusted p-value : 0.257 #> --- #> Signif. codes: '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 #> ---------------------------------------------#> Performing simulations under the model. #> Plotting VPC #> Method used for VPC: binning by quantiles on X , dividing into the following intervals #> Interval Centered.On #> 1 (-1,3] 1.3 #> 2 (3,8] 7.4 #> 3 (8,14] 13.2 #> 4 (14,21] 20.5 #> 5 (21,37.7] 29.5 #> 6 (37.7,60] 50.4 #> 7 (60,90] 76.6 #> 8 (90,120] 109.0 #> 9 (120,180] 156.0f_mmkin_parent_tc <- update(f_mmkin_parent, error_model = "tc") f_saem_fomc_tc <- saem(f_mmkin_parent_tc["FOMC", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:15 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:20 2020"#> Likelihoods computed by importance sampling#> AIC BIC #> 1 467.7096 464.9757 #> 2 469.5208 466.3963#>#>#># The following fit uses analytical solutions for SFO-SFO and DFOP-SFO, # and compiled ODEs for FOMC that are much slower f_mmkin <- mmkin(list( "SFO-SFO" = sfo_sfo, "FOMC-SFO" = fomc_sfo, "DFOP-SFO" = dfop_sfo), ds, quiet = TRUE) # These take about five seconds each on this system, as we use # analytical solutions written for saemix. When using the analytical # solutions written for mkin this took around four minutes f_saem_sfo_sfo <- saem(f_mmkin["SFO-SFO", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:23 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:28 2020"f_saem_dfop_sfo <- saem(f_mmkin["DFOP-SFO", ])#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:29 2020" #> .... #> Minimisation finished #> [1] "Mon Nov 30 15:53:38 2020"#> Kinetic nonlinear mixed-effects model fit by SAEM #> Structural model: #> d_parent/dt = - ((k1 * g * exp(-k1 * time) + k2 * (1 - g) * exp(-k2 * #> time)) / (g * exp(-k1 * time) + (1 - g) * exp(-k2 * time))) #> * parent #> d_A1/dt = + f_parent_to_A1 * ((k1 * g * exp(-k1 * time) + k2 * (1 - g) #> * exp(-k2 * time)) / (g * exp(-k1 * time) + (1 - g) * #> exp(-k2 * time))) * parent - k_A1 * A1 #> #> Data: #> 170 observations of 2 variable(s) grouped in 5 datasets #> #> Likelihood computed by importance sampling #> AIC BIC logLik #> 841.6 836.5 -407.8 #> #> Fitted parameters: #> estimate lower upper #> parent_0 93.76647 91.15312 96.3798 #> log_k_A1 -6.13235 -8.45788 -3.8068 #> f_parent_qlogis -0.97364 -1.36940 -0.5779 #> log_k1 -2.53176 -3.80372 -1.2598 #> log_k2 -3.58667 -5.29524 -1.8781 #> g_qlogis 0.01238 -1.07968 1.1044 #> Var.parent_0 7.61106 -3.34955 18.5717 #> Var.log_k_A1 4.64679 -2.73133 12.0249 #> Var.f_parent_qlogis 0.19693 -0.05498 0.4488 #> Var.log_k1 2.01717 -0.51980 4.5542 #> Var.log_k2 3.63412 -0.92964 8.1979 #> Var.g_qlogis 0.20045 -0.97425 1.3751 #> a.1 1.88335 1.66636 2.1004 #> SD.parent_0 2.75881 0.77234 4.7453 #> SD.log_k_A1 2.15564 0.44429 3.8670 #> SD.f_parent_qlogis 0.44377 0.15994 0.7276 #> SD.log_k1 1.42027 0.52714 2.3134 #> SD.log_k2 1.90634 0.70934 3.1033 #> SD.g_qlogis 0.44771 -0.86417 1.7596#> saemix version used for fitting: 3.1.9000 #> mkin version used for pre-fitting: 0.9.50.4 #> R version used for fitting: 4.0.3 #> Date of fit: Mon Nov 30 15:53:38 2020 #> Date of summary: Mon Nov 30 15:53:39 2020 #> #> Equations: #> d_parent/dt = - ((k1 * g * exp(-k1 * time) + k2 * (1 - g) * exp(-k2 * #> time)) / (g * exp(-k1 * time) + (1 - g) * exp(-k2 * time))) #> * parent #> d_A1/dt = + f_parent_to_A1 * ((k1 * g * exp(-k1 * time) + k2 * (1 - g) #> * exp(-k2 * time)) / (g * exp(-k1 * time) + (1 - g) * #> exp(-k2 * time))) * parent - k_A1 * A1 #> #> Data: #> 170 observations of 2 variable(s) grouped in 5 datasets #> #> Model predictions using solution type analytical #> #> Fitted in 9.963 s using 300, 100 iterations #> #> Variance model: Constant variance #> #> Mean of starting values for individual parameters: #> parent_0 log_k_A1 f_parent_qlogis log_k1 log_k2 #> 93.8101519 -9.7647455 -0.9711148 -1.8799371 -4.2708142 #> g_qlogis #> 0.1356441 #> #> Fixed degradation parameter values: #> None #> #> Results: #> #> Likelihood computed by importance sampling #> AIC BIC logLik #> 841.6 836.5 -407.8 #> #> Optimised, transformed parameters with symmetric confidence intervals: #> est. lower upper #> parent_0 93.76647 91.153 96.3798 #> log_k_A1 -6.13235 -8.458 -3.8068 #> f_parent_qlogis -0.97364 -1.369 -0.5779 #> log_k1 -2.53176 -3.804 -1.2598 #> log_k2 -3.58667 -5.295 -1.8781 #> g_qlogis 0.01238 -1.080 1.1044 #> #> Correlation: #> prnt_0 lg__A1 f_prn_ log_k1 log_k2 #> log_k_A1 -0.013 #> f_parent_qlogis -0.025 0.050 #> log_k1 0.030 0.000 -0.005 #> log_k2 0.010 0.005 -0.003 0.032 #> g_qlogis -0.063 -0.015 0.010 -0.167 -0.177 #> #> Random effects: #> est. lower upper #> SD.parent_0 2.7588 0.7723 4.7453 #> SD.log_k_A1 2.1556 0.4443 3.8670 #> SD.f_parent_qlogis 0.4438 0.1599 0.7276 #> SD.log_k1 1.4203 0.5271 2.3134 #> SD.log_k2 1.9063 0.7093 3.1033 #> SD.g_qlogis 0.4477 -0.8642 1.7596 #> #> Variance model: #> est. lower upper #> a.1 1.883 1.666 2.1 #> #> Backtransformed parameters with asymmetric confidence intervals: #> est. lower upper #> parent_0 93.766473 9.115e+01 96.37983 #> k_A1 0.002171 2.122e-04 0.02222 #> f_parent_to_A1 0.274156 2.027e-01 0.35942 #> k1 0.079519 2.229e-02 0.28371 #> k2 0.027691 5.015e-03 0.15288 #> g 0.503095 2.536e-01 0.75109 #> #> Resulting formation fractions: #> ff #> parent_A1 0.2742 #> parent_sink 0.7258 #> #> Estimated disappearance times: #> DT50 DT90 DT50back DT50_k1 DT50_k2 #> parent 14.11 59.53 17.92 8.717 25.03 #> A1 319.21 1060.38 NA NA NA #> #> Data: #> ds name time observed predicted residual std standardized #> Dataset 6 parent 0 97.2 95.79523 -1.40477 1.883 -0.745888 #> Dataset 6 parent 0 96.4 95.79523 -0.60477 1.883 -0.321114 #> Dataset 6 parent 3 71.1 71.32042 0.22042 1.883 0.117035 #> Dataset 6 parent 3 69.2 71.32042 2.12042 1.883 1.125873 #> Dataset 6 parent 6 58.1 56.45256 -1.64744 1.883 -0.874739 #> Dataset 6 parent 6 56.6 56.45256 -0.14744 1.883 -0.078288 #> Dataset 6 parent 10 44.4 44.48523 0.08523 1.883 0.045256 #> Dataset 6 parent 10 43.4 44.48523 1.08523 1.883 0.576224 #> Dataset 6 parent 20 33.3 29.75774 -3.54226 1.883 -1.880826 #> Dataset 6 parent 20 29.2 29.75774 0.55774 1.883 0.296141 #> Dataset 6 parent 34 17.6 19.35710 1.75710 1.883 0.932966 #> Dataset 6 parent 34 18.0 19.35710 1.35710 1.883 0.720578 #> Dataset 6 parent 55 10.5 10.48443 -0.01557 1.883 -0.008266 #> Dataset 6 parent 55 9.3 10.48443 1.18443 1.883 0.628895 #> Dataset 6 parent 90 4.5 3.78622 -0.71378 1.883 -0.378995 #> Dataset 6 parent 90 4.7 3.78622 -0.91378 1.883 -0.485188 #> Dataset 6 parent 112 3.0 1.99608 -1.00392 1.883 -0.533048 #> Dataset 6 parent 112 3.4 1.99608 -1.40392 1.883 -0.745435 #> Dataset 6 parent 132 2.3 1.11539 -1.18461 1.883 -0.628990 #> Dataset 6 parent 132 2.7 1.11539 -1.58461 1.883 -0.841377 #> Dataset 6 A1 3 4.3 4.66132 0.36132 1.883 0.191849 #> Dataset 6 A1 3 4.6 4.66132 0.06132 1.883 0.032559 #> Dataset 6 A1 6 7.0 7.41087 0.41087 1.883 0.218157 #> Dataset 6 A1 6 7.2 7.41087 0.21087 1.883 0.111964 #> Dataset 6 A1 10 8.2 9.50878 1.30878 1.883 0.694921 #> Dataset 6 A1 10 8.0 9.50878 1.50878 1.883 0.801114 #> Dataset 6 A1 20 11.0 11.69902 0.69902 1.883 0.371157 #> Dataset 6 A1 20 13.7 11.69902 -2.00098 1.883 -1.062455 #> Dataset 6 A1 34 11.5 12.67784 1.17784 1.883 0.625396 #> Dataset 6 A1 34 12.7 12.67784 -0.02216 1.883 -0.011765 #> Dataset 6 A1 55 14.9 12.78556 -2.11444 1.883 -1.122701 #> Dataset 6 A1 55 14.5 12.78556 -1.71444 1.883 -0.910314 #> Dataset 6 A1 90 12.1 11.52954 -0.57046 1.883 -0.302898 #> Dataset 6 A1 90 12.3 11.52954 -0.77046 1.883 -0.409092 #> Dataset 6 A1 112 9.9 10.43825 0.53825 1.883 0.285793 #> Dataset 6 A1 112 10.2 10.43825 0.23825 1.883 0.126503 #> Dataset 6 A1 132 8.8 9.42830 0.62830 1.883 0.333609 #> Dataset 6 A1 132 7.8 9.42830 1.62830 1.883 0.864577 #> Dataset 7 parent 0 93.6 90.91477 -2.68523 1.883 -1.425772 #> Dataset 7 parent 0 92.3 90.91477 -1.38523 1.883 -0.735514 #> Dataset 7 parent 3 87.0 84.76874 -2.23126 1.883 -1.184726 #> Dataset 7 parent 3 82.2 84.76874 2.56874 1.883 1.363919 #> Dataset 7 parent 7 74.0 77.62735 3.62735 1.883 1.926003 #> Dataset 7 parent 7 73.9 77.62735 3.72735 1.883 1.979100 #> Dataset 7 parent 14 64.2 67.52266 3.32266 1.883 1.764224 #> Dataset 7 parent 14 69.5 67.52266 -1.97734 1.883 -1.049904 #> Dataset 7 parent 30 54.0 52.41949 -1.58051 1.883 -0.839202 #> Dataset 7 parent 30 54.6 52.41949 -2.18051 1.883 -1.157783 #> Dataset 7 parent 60 41.1 39.36582 -1.73418 1.883 -0.920794 #> Dataset 7 parent 60 38.4 39.36582 0.96582 1.883 0.512818 #> Dataset 7 parent 90 32.5 33.75388 1.25388 1.883 0.665771 #> Dataset 7 parent 90 35.5 33.75388 -1.74612 1.883 -0.927132 #> Dataset 7 parent 120 28.1 30.41716 2.31716 1.883 1.230335 #> Dataset 7 parent 120 29.0 30.41716 1.41716 1.883 0.752464 #> Dataset 7 parent 180 26.5 25.66046 -0.83954 1.883 -0.445767 #> Dataset 7 parent 180 27.6 25.66046 -1.93954 1.883 -1.029832 #> Dataset 7 A1 3 3.9 2.69355 -1.20645 1.883 -0.640585 #> Dataset 7 A1 3 3.1 2.69355 -0.40645 1.883 -0.215811 #> Dataset 7 A1 7 6.9 5.81807 -1.08193 1.883 -0.574470 #> Dataset 7 A1 7 6.6 5.81807 -0.78193 1.883 -0.415180 #> Dataset 7 A1 14 10.4 10.22529 -0.17471 1.883 -0.092767 #> Dataset 7 A1 14 8.3 10.22529 1.92529 1.883 1.022265 #> Dataset 7 A1 30 14.4 16.75484 2.35484 1.883 1.250345 #> Dataset 7 A1 30 13.7 16.75484 3.05484 1.883 1.622022 #> Dataset 7 A1 60 22.1 22.22540 0.12540 1.883 0.066583 #> Dataset 7 A1 60 22.3 22.22540 -0.07460 1.883 -0.039610 #> Dataset 7 A1 90 27.5 24.38799 -3.11201 1.883 -1.652376 #> Dataset 7 A1 90 25.4 24.38799 -1.01201 1.883 -0.537344 #> Dataset 7 A1 120 28.0 25.53294 -2.46706 1.883 -1.309927 #> Dataset 7 A1 120 26.6 25.53294 -1.06706 1.883 -0.566572 #> Dataset 7 A1 180 25.8 26.94943 1.14943 1.883 0.610309 #> Dataset 7 A1 180 25.3 26.94943 1.64943 1.883 0.875793 #> Dataset 8 parent 0 91.9 91.53246 -0.36754 1.883 -0.195151 #> Dataset 8 parent 0 90.8 91.53246 0.73246 1.883 0.388914 #> Dataset 8 parent 1 64.9 67.73197 2.83197 1.883 1.503686 #> Dataset 8 parent 1 66.2 67.73197 1.53197 1.883 0.813428 #> Dataset 8 parent 3 43.5 41.58448 -1.91552 1.883 -1.017081 #> Dataset 8 parent 3 44.1 41.58448 -2.51552 1.883 -1.335661 #> Dataset 8 parent 8 18.3 19.62286 1.32286 1.883 0.702395 #> Dataset 8 parent 8 18.1 19.62286 1.52286 1.883 0.808589 #> Dataset 8 parent 14 10.2 10.77819 0.57819 1.883 0.306999 #> Dataset 8 parent 14 10.8 10.77819 -0.02181 1.883 -0.011582 #> Dataset 8 parent 27 4.9 3.26977 -1.63023 1.883 -0.865599 #> Dataset 8 parent 27 3.3 3.26977 -0.03023 1.883 -0.016051 #> Dataset 8 parent 48 1.6 0.48024 -1.11976 1.883 -0.594557 #> Dataset 8 parent 48 1.5 0.48024 -1.01976 1.883 -0.541460 #> Dataset 8 parent 70 1.1 0.06438 -1.03562 1.883 -0.549881 #> Dataset 8 parent 70 0.9 0.06438 -0.83562 1.883 -0.443688 #> Dataset 8 A1 1 9.6 7.61539 -1.98461 1.883 -1.053761 #> Dataset 8 A1 1 7.7 7.61539 -0.08461 1.883 -0.044923 #> Dataset 8 A1 3 15.0 15.47954 0.47954 1.883 0.254622 #> Dataset 8 A1 3 15.1 15.47954 0.37954 1.883 0.201525 #> Dataset 8 A1 8 21.2 20.22616 -0.97384 1.883 -0.517076 #> Dataset 8 A1 8 21.1 20.22616 -0.87384 1.883 -0.463979 #> Dataset 8 A1 14 19.7 20.00067 0.30067 1.883 0.159645 #> Dataset 8 A1 14 18.9 20.00067 1.10067 1.883 0.584419 #> Dataset 8 A1 27 17.5 16.38142 -1.11858 1.883 -0.593929 #> Dataset 8 A1 27 15.9 16.38142 0.48142 1.883 0.255619 #> Dataset 8 A1 48 9.5 10.25357 0.75357 1.883 0.400123 #> Dataset 8 A1 48 9.8 10.25357 0.45357 1.883 0.240833 #> Dataset 8 A1 70 6.2 5.95728 -0.24272 1.883 -0.128878 #> Dataset 8 A1 70 6.1 5.95728 -0.14272 1.883 -0.075781 #> Dataset 9 parent 0 99.8 97.47274 -2.32726 1.883 -1.235697 #> Dataset 9 parent 0 98.3 97.47274 -0.82726 1.883 -0.439246 #> Dataset 9 parent 1 77.1 79.72257 2.62257 1.883 1.392500 #> Dataset 9 parent 1 77.2 79.72257 2.52257 1.883 1.339404 #> Dataset 9 parent 3 59.0 56.26497 -2.73503 1.883 -1.452212 #> Dataset 9 parent 3 58.1 56.26497 -1.83503 1.883 -0.974342 #> Dataset 9 parent 8 27.4 31.66985 4.26985 1.883 2.267151 #> Dataset 9 parent 8 29.2 31.66985 2.46985 1.883 1.311410 #> Dataset 9 parent 14 19.1 22.39789 3.29789 1.883 1.751071 #> Dataset 9 parent 14 29.6 22.39789 -7.20211 1.883 -3.824090 #> Dataset 9 parent 27 10.1 14.21758 4.11758 1.883 2.186301 #> Dataset 9 parent 27 18.2 14.21758 -3.98242 1.883 -2.114537 #> Dataset 9 parent 48 4.5 7.27921 2.77921 1.883 1.475671 #> Dataset 9 parent 48 9.1 7.27921 -1.82079 1.883 -0.966780 #> Dataset 9 parent 70 2.3 3.61470 1.31470 1.883 0.698065 #> Dataset 9 parent 70 2.9 3.61470 0.71470 1.883 0.379485 #> Dataset 9 parent 91 2.0 1.85303 -0.14697 1.883 -0.078038 #> Dataset 9 parent 91 1.8 1.85303 0.05303 1.883 0.028155 #> Dataset 9 parent 120 2.0 0.73645 -1.26355 1.883 -0.670906 #> Dataset 9 parent 120 2.2 0.73645 -1.46355 1.883 -0.777099 #> Dataset 9 A1 1 4.2 3.87843 -0.32157 1.883 -0.170743 #> Dataset 9 A1 1 3.9 3.87843 -0.02157 1.883 -0.011453 #> Dataset 9 A1 3 7.4 8.90535 1.50535 1.883 0.799291 #> Dataset 9 A1 3 7.9 8.90535 1.00535 1.883 0.533807 #> Dataset 9 A1 8 14.5 13.75172 -0.74828 1.883 -0.397312 #> Dataset 9 A1 8 13.7 13.75172 0.05172 1.883 0.027462 #> Dataset 9 A1 14 14.2 14.97541 0.77541 1.883 0.411715 #> Dataset 9 A1 14 12.2 14.97541 2.77541 1.883 1.473650 #> Dataset 9 A1 27 13.7 14.94728 1.24728 1.883 0.662266 #> Dataset 9 A1 27 13.2 14.94728 1.74728 1.883 0.927750 #> Dataset 9 A1 48 13.6 13.66078 0.06078 1.883 0.032272 #> Dataset 9 A1 48 15.4 13.66078 -1.73922 1.883 -0.923470 #> Dataset 9 A1 70 10.4 11.84899 1.44899 1.883 0.769365 #> Dataset 9 A1 70 11.6 11.84899 0.24899 1.883 0.132204 #> Dataset 9 A1 91 10.0 10.09177 0.09177 1.883 0.048727 #> Dataset 9 A1 91 9.5 10.09177 0.59177 1.883 0.314211 #> Dataset 9 A1 120 9.1 7.91379 -1.18621 1.883 -0.629841 #> Dataset 9 A1 120 9.0 7.91379 -1.08621 1.883 -0.576745 #> Dataset 10 parent 0 96.1 93.65257 -2.44743 1.883 -1.299505 #> Dataset 10 parent 0 94.3 93.65257 -0.64743 1.883 -0.343763 #> Dataset 10 parent 8 73.9 77.85906 3.95906 1.883 2.102132 #> Dataset 10 parent 8 73.9 77.85906 3.95906 1.883 2.102132 #> Dataset 10 parent 14 69.4 70.17143 0.77143 1.883 0.409606 #> Dataset 10 parent 14 73.1 70.17143 -2.92857 1.883 -1.554974 #> Dataset 10 parent 21 65.6 63.99188 -1.60812 1.883 -0.853862 #> Dataset 10 parent 21 65.3 63.99188 -1.30812 1.883 -0.694572 #> Dataset 10 parent 41 55.9 54.64292 -1.25708 1.883 -0.667467 #> Dataset 10 parent 41 54.4 54.64292 0.24292 1.883 0.128985 #> Dataset 10 parent 63 47.0 49.61303 2.61303 1.883 1.387433 #> Dataset 10 parent 63 49.3 49.61303 0.31303 1.883 0.166207 #> Dataset 10 parent 91 44.7 45.17807 0.47807 1.883 0.253839 #> Dataset 10 parent 91 46.7 45.17807 -1.52193 1.883 -0.808096 #> Dataset 10 parent 120 42.1 41.27970 -0.82030 1.883 -0.435552 #> Dataset 10 parent 120 41.3 41.27970 -0.02030 1.883 -0.010778 #> Dataset 10 A1 8 3.3 3.99294 0.69294 1.883 0.367929 #> Dataset 10 A1 8 3.4 3.99294 0.59294 1.883 0.314832 #> Dataset 10 A1 14 3.9 5.92756 2.02756 1.883 1.076570 #> Dataset 10 A1 14 2.9 5.92756 3.02756 1.883 1.607538 #> Dataset 10 A1 21 6.4 7.47313 1.07313 1.883 0.569799 #> Dataset 10 A1 21 7.2 7.47313 0.27313 1.883 0.145025 #> Dataset 10 A1 41 9.1 9.76819 0.66819 1.883 0.354786 #> Dataset 10 A1 41 8.5 9.76819 1.26819 1.883 0.673367 #> Dataset 10 A1 63 11.7 10.94733 -0.75267 1.883 -0.399643 #> Dataset 10 A1 63 12.0 10.94733 -1.05267 1.883 -0.558933 #> Dataset 10 A1 91 13.3 11.93773 -1.36227 1.883 -0.723321 #> Dataset 10 A1 91 13.2 11.93773 -1.26227 1.883 -0.670224 #> Dataset 10 A1 120 14.3 12.77666 -1.52334 1.883 -0.808847 #> Dataset 10 A1 120 12.1 12.77666 0.67666 1.883 0.359282# Using a single core, the following takes about 6 minutes as we do not have an # analytical solution. Using 10 cores it is slower instead of faster f_saem_fomc <- saem(f_mmkin["FOMC-SFO", ], cores = 1)#> Running main SAEM algorithm #> [1] "Mon Nov 30 15:53:39 2020" #> DLSODA- At current T (=R1), MXSTEP (=I1) steps #> taken on this call before reaching TOUT #> In above message, I1 = 5000 #> #> In above message, R1 = 0.00156238 #> #> DLSODA- At T (=R1) and step size H (=R2), the #> corrector convergence failed repeatedly #> or with ABS(H) = HMIN #> In above message, R1 = 0, R2 = 1.1373e-10 #> #> DLSODA- At current T (=R1), MXSTEP (=I1) steps #> taken on this call before reaching TOUT #> In above message, I1 = 5000 #> #> In above message, R1 = 2.24752e-06 #> #> .... #> Minimisation finished #> [1] "Mon Nov 30 16:00:45 2020"# }