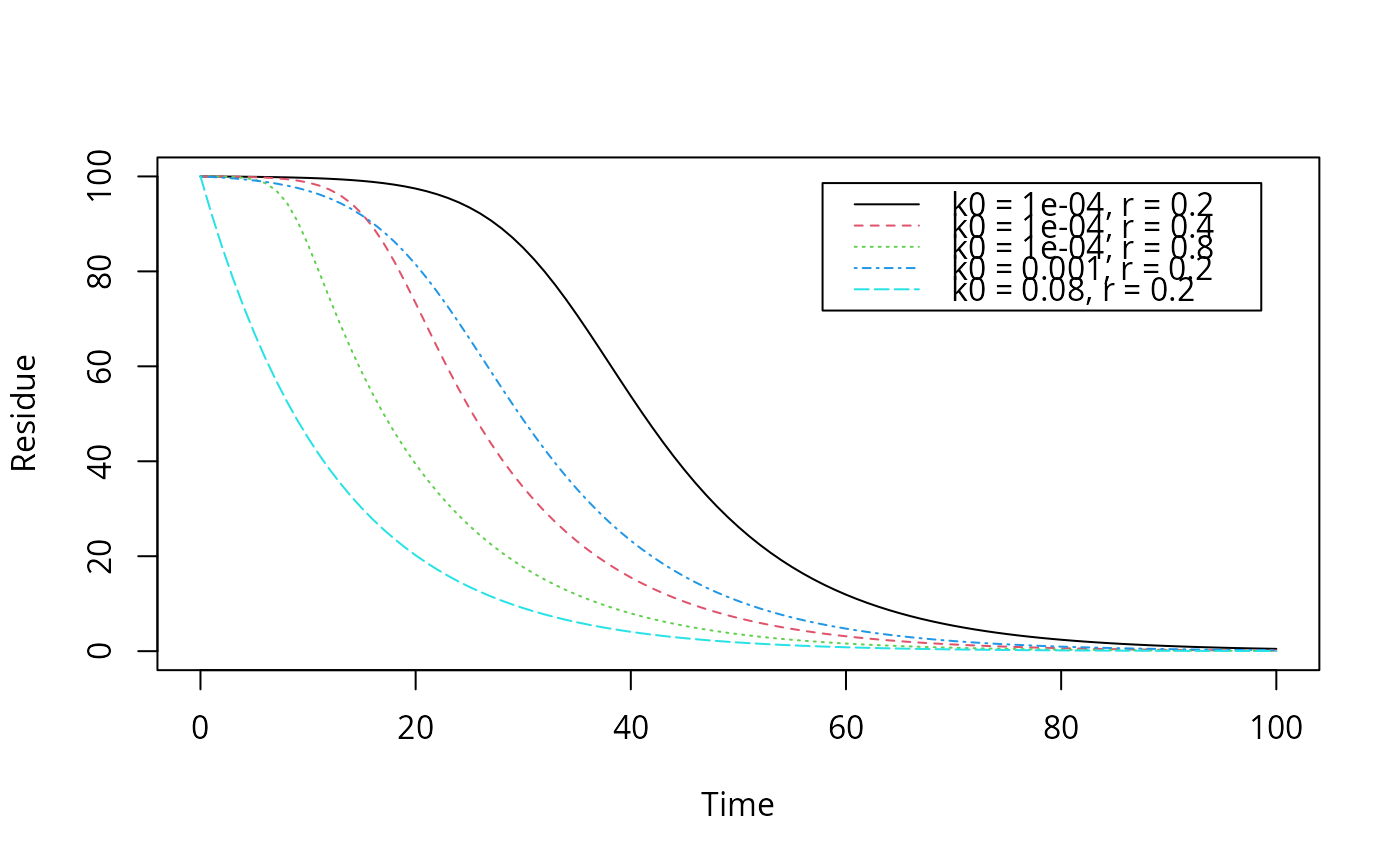
Logistic kinetics
logistic.solution.RdFunction describing exponential decline from a defined starting value, with an increasing rate constant, supposedly caused by microbial growth
logistic.solution(t, parent.0, kmax, k0, r)
Arguments
| t | Time. |
|---|---|
| parent.0 | Starting value for the response variable at time zero. |
| kmax | Maximum rate constant. |
| k0 | Minumum rate constant effective at time zero. |
| r | Growth rate of the increase in the rate constant. |
Note
The solution of the logistic model reduces to the
SFO.solution if k0 is equal to
kmax.
Value
The value of the response variable at time t.
References
FOCUS (2014) “Generic guidance for Estimating Persistence and Degradation Kinetics from Environmental Fate Studies on Pesticides in EU Registration” Report of the FOCUS Work Group on Degradation Kinetics, Version 1.1, 18 December 2014 http://esdac.jrc.ec.europa.eu/projects/degradation-kinetics
Examples
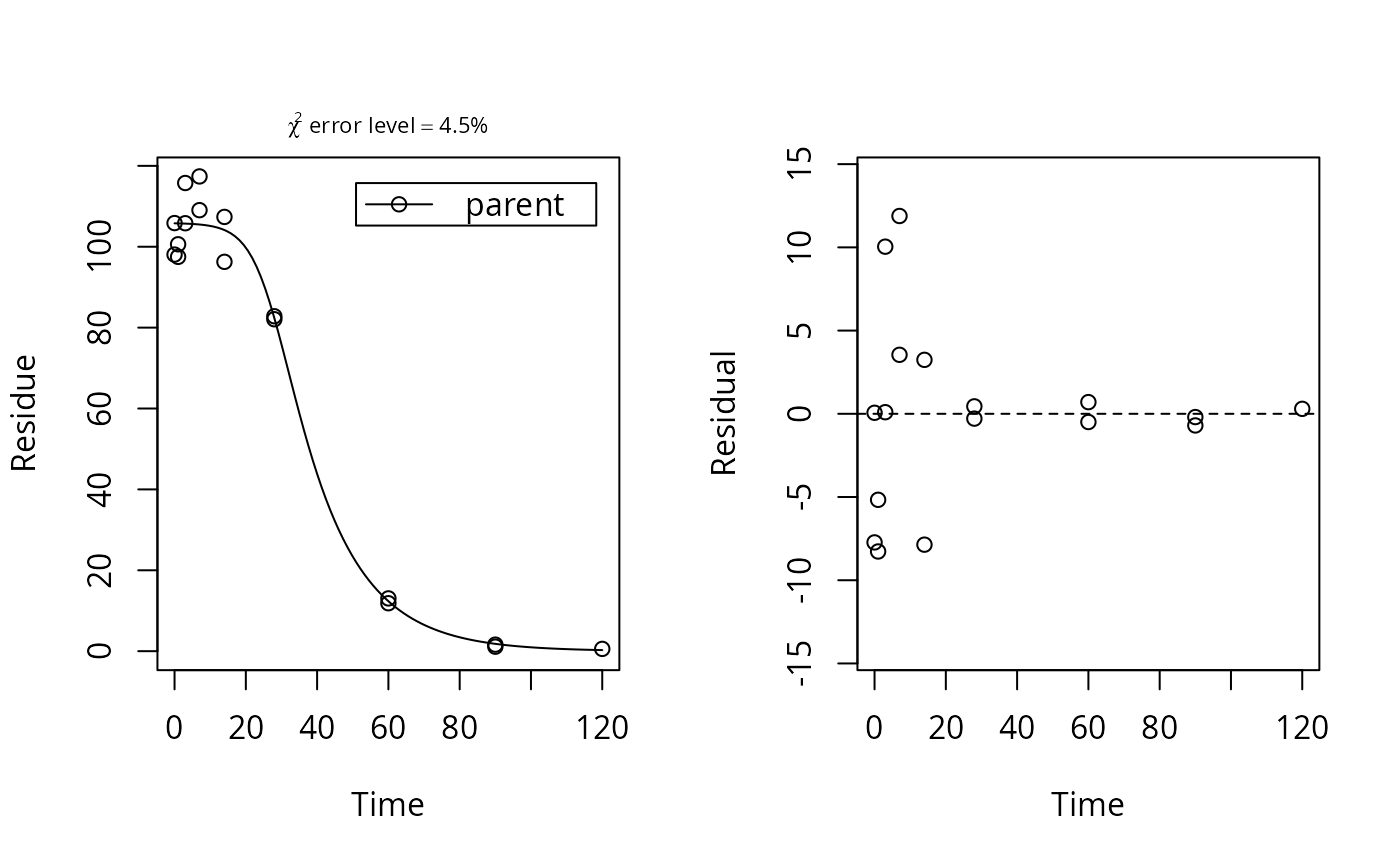
# Reproduce the plot on page 57 of FOCUS (2014) plot(function(x) logistic.solution(x, 100, 0.08, 0.0001, 0.2), from = 0, to = 100, ylim = c(0, 100), xlab = "Time", ylab = "Residue")plot(function(x) logistic.solution(x, 100, 0.08, 0.0001, 0.4), from = 0, to = 100, add = TRUE, lty = 2, col = 2)plot(function(x) logistic.solution(x, 100, 0.08, 0.0001, 0.8), from = 0, to = 100, add = TRUE, lty = 3, col = 3)plot(function(x) logistic.solution(x, 100, 0.08, 0.001, 0.2), from = 0, to = 100, add = TRUE, lty = 4, col = 4)plot(function(x) logistic.solution(x, 100, 0.08, 0.08, 0.2), from = 0, to = 100, add = TRUE, lty = 5, col = 5)legend("topright", inset = 0.05, legend = paste0("k0 = ", c(0.0001, 0.0001, 0.0001, 0.001, 0.08), ", r = ", c(0.2, 0.4, 0.8, 0.2, 0.2)), lty = 1:5, col = 1:5)# Fit with synthetic data logistic <- mkinmod(parent = mkinsub("logistic")) sampling_times = c(0, 1, 3, 7, 14, 28, 60, 90, 120) parms_logistic <- c(kmax = 0.08, k0 = 0.0001, r = 0.2) parms_logistic_optim <- c(parent_0 = 100, parms_logistic) d_logistic <- mkinpredict(logistic, parms_logistic, c(parent = 100), sampling_times) d_2_1 <- add_err(d_logistic, sdfunc = function(x) sigma_twocomp(x, 0.5, 0.07), n = 1, reps = 2, digits = 5, LOD = 0.1, seed = 123456)[[1]] m <- mkinfit("logistic", d_2_1)#> Model cost at call 1 : 789.6044 #> Model cost at call 2 : 789.6043 #> Model cost at call 7 : 716.9934 #> Model cost at call 12 : 697.1186 #> Model cost at call 15 : 697.1185 #> Model cost at call 16 : 697.1184 #> Model cost at call 17 : 661.1574 #> Model cost at call 20 : 661.1573 #> Model cost at call 22 : 620.0542 #> Model cost at call 25 : 620.0541 #> Model cost at call 29 : 616.6874 #> Model cost at call 32 : 616.6874 #> Model cost at call 33 : 616.6874 #> Model cost at call 34 : 615.1671 #> Model cost at call 37 : 615.1671 #> Model cost at call 39 : 612.0795 #> Model cost at call 42 : 612.0795 #> Model cost at call 43 : 612.0795 #> Model cost at call 44 : 605.9119 #> Model cost at call 45 : 593.0433 #> Model cost at call 46 : 548.0815 #> Model cost at call 47 : 504.9062 #> Model cost at call 50 : 504.9061 #> Model cost at call 51 : 504.9061 #> Model cost at call 53 : 485.929 #> Model cost at call 55 : 485.929 #> Model cost at call 56 : 485.929 #> Model cost at call 58 : 485.241 #> Model cost at call 60 : 485.241 #> Model cost at call 61 : 485.2409 #> Model cost at call 62 : 485.2409 #> Model cost at call 63 : 484.0717 #> Model cost at call 69 : 483.9062 #> Model cost at call 74 : 483.5646 #> Model cost at call 79 : 483.4908 #> Model cost at call 84 : 483.4859 #> Model cost at call 85 : 483.4859 #> Model cost at call 89 : 483.4848 #> Model cost at call 90 : 483.4836 #> Model cost at call 92 : 483.4836 #> Model cost at call 94 : 483.4836 #> Model cost at call 97 : 483.4833 #> Model cost at call 100 : 483.4833 #> Model cost at call 105 : 483.4832 #> Model cost at call 108 : 483.4832 #> Model cost at call 114 : 483.4832 #> Model cost at call 128 : 483.4832 #> Optimisation by method Port successfully terminated.plot_sep(m)#> Estimate se_notrans t value Pr(>t) Lower #> parent_0 1.057896e+02 2.3743105248 44.5559374 6.656664e-16 1.006602e+02 #> kmax 6.398190e-02 0.0193490291 3.3067243 2.836921e-03 3.329058e-02 #> k0 1.612775e-04 0.0009640761 0.1672871 4.348592e-01 3.972250e-10 #> r 2.263946e-01 0.2822811886 0.8020181 2.184792e-01 1.531165e-02 #> Upper #> parent_0 110.9190170 #> kmax 0.1229682 #> k0 65.4803698 #> r 3.3474197