Skip to contents

Two-component error model

Source: R/sigma_twocomp.R
sigma_twocomp.Rd

Function describing the standard deviation of the measurement error in dependence of the measured value \(y\):

Usage

sigma_twocomp(y, sigma_low, rsd_high)

Arguments

y

The magnitude of the observed value

sigma_low

The asymptotic minimum of the standard deviation for low observed values

rsd_high

The coefficient describing the increase of the standard deviation with the magnitude of the observed value

Value

The standard deviation of the response variable.

Details

$$\sigma = \sqrt{ \sigma_{low}^2 + y^2 * {rsd}_{high}^2}$$ sigma = sqrt(sigma_low^2 + y^2 * rsd_high^2)

This is the error model used for example by Werner et al. (1978). The model proposed by Rocke and Lorenzato (1995) can be written in this form as well, but assumes approximate lognormal distribution of errors for high values of y.

References

Werner, Mario, Brooks, Samuel H., and Knott, Lancaster B. (1978) Additive, Multiplicative, and Mixed Analytical Errors. Clinical Chemistry 24(11), 1895-1898.

Rocke, David M. and Lorenzato, Stefan (1995) A two-component model for measurement error in analytical chemistry. Technometrics 37(2), 176-184.

Ranke J and Meinecke S (2019) Error Models for the Kinetic Evaluation of Chemical Degradation Data. Environments 6(12) 124 doi:10.3390/environments6120124 .

Examples

times <- c(0, 1, 3, 7, 14, 28, 60, 90, 120)
d_pred <- data.frame(time = times, parent = 100 * exp(- 0.03 * times))
set.seed(123456)
d_syn <- add_err(d_pred, function(y) sigma_twocomp(y, 1, 0.07),
  reps = 2, n = 1)[[1]]
f_nls <- nls(value ~ SSasymp(time, 0, parent_0, lrc), data = d_syn,
 start = list(parent_0 = 100, lrc = -3))
library(nlme)
f_gnls <- gnls(value ~ SSasymp(time, 0, parent_0, lrc),
  data = d_syn, na.action = na.omit,
  start = list(parent_0 = 100, lrc = -3))
if (length(findFunction("varConstProp")) > 0) {
  f_gnls_tc <- update(f_gnls, weights = varConstProp())
  f_gnls_tc_sf <- update(f_gnls_tc, control = list(sigma = 1))
}
f_mkin <- mkinfit("SFO", d_syn, error_model = "const", quiet = TRUE)
f_mkin_tc <- mkinfit("SFO", d_syn, error_model = "tc", quiet = TRUE)
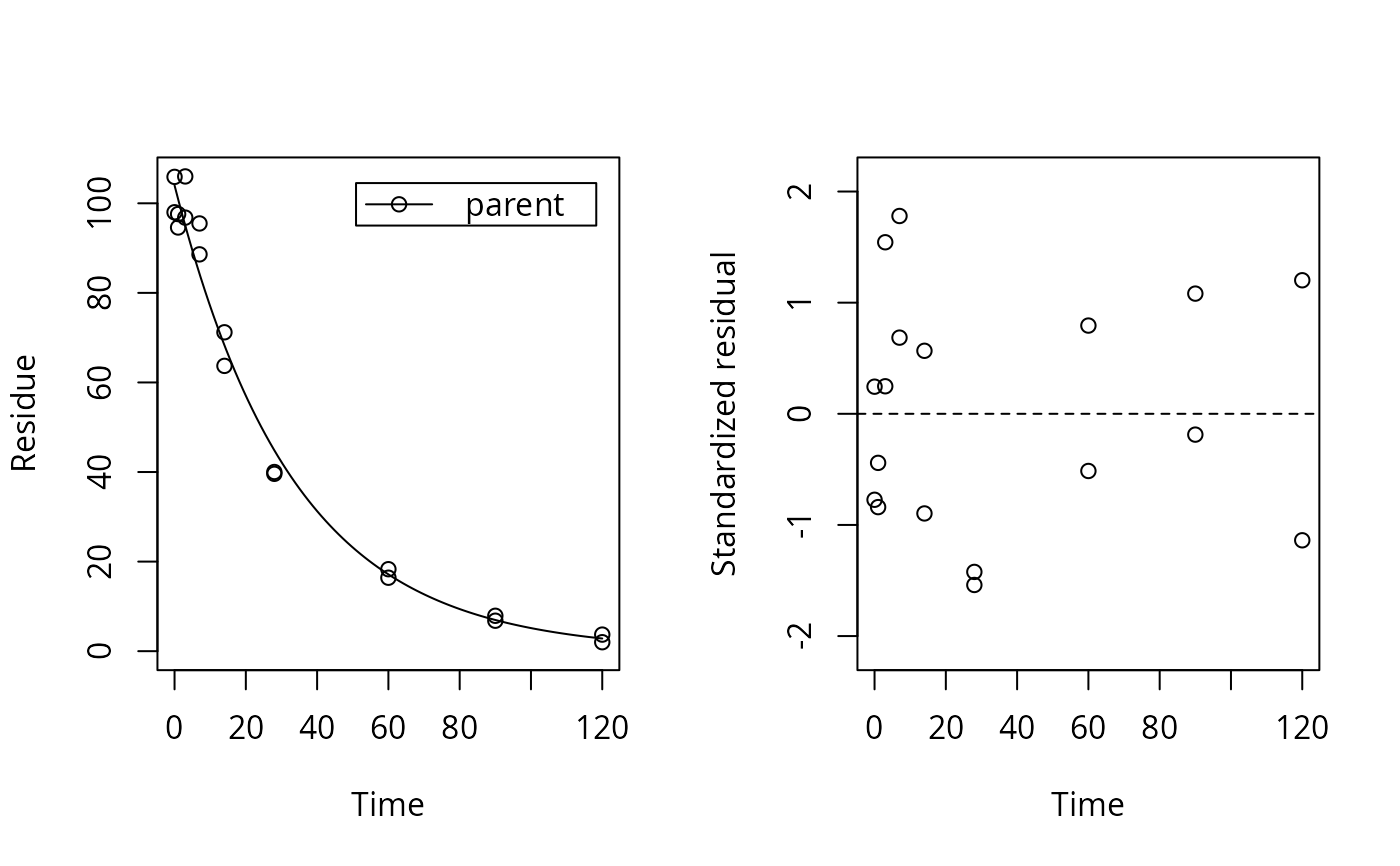
plot_res(f_mkin_tc, standardized = TRUE)

AIC(f_nls, f_gnls, f_gnls_tc, f_gnls_tc_sf, f_mkin, f_mkin_tc)
#>              df      AIC
#> f_nls         3 114.4817
#> f_gnls        3 114.4817
#> f_gnls_tc     5 103.6447
#> f_gnls_tc_sf  4 101.6447
#> f_mkin        3 114.4817
#> f_mkin_tc     4 101.6446